题目内容
已知函数f(x)=2
sinωxcosωx-2sin2ωx+1(ω>0)的最小正周期为π,
(Ⅰ)当x∈[0,
]时,求函数f(x)的取值范围;
(Ⅱ)若α是锐角,且f(
-
)=
,求cosα的值.
| 3 |
(Ⅰ)当x∈[0,
| π |
| 2 |
(Ⅱ)若α是锐角,且f(
| a |
| 2 |
| π |
| 6 |
| 6 |
| 5 |
(I)函数f(x)=2
sinωxcosωx-2sin2ωx+1
=
sin2ωx-2×
+1
=2sin(2ωx+
).
因为函数f(x)的最小正周期为π,即
=π,∴ω=1.
∴f(x)=2sin(2x+
).
∵x∈[0,
],∴2x+
∈[
,
],2sin(2x+
)∈[-1,2].
∴f(x)的取值范围为[-1,2].
(II)由(1)可知f(
-
)=2sin(α-
)=
,
∴sin(α-
)=
,∵α是锐角
∴cos(α-
)=
,
∴cosα=cos[(α-
)+
]
=cos(α-
)cos
-sin(α-
)sin
=
×
-
×
=
.
| 3 |
=
| 3 |
| 1-cos2ωx |
| 2 |
=2sin(2ωx+
| π |
| 6 |
因为函数f(x)的最小正周期为π,即
| 2π |
| 2ω |
∴f(x)=2sin(2x+
| π |
| 6 |
∵x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
∴f(x)的取值范围为[-1,2].
(II)由(1)可知f(
| a |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 6 |
| 5 |
∴sin(α-
| π |
| 6 |
| 3 |
| 5 |
∴cos(α-
| π |
| 6 |
| 4 |
| 5 |
∴cosα=cos[(α-
| π |
| 6 |
| π |
| 6 |
=cos(α-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
4
| ||
| 10 |

练习册系列答案
相关题目
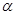 的终边在第一象限,函数
的终边在第一象限,函数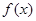 的定义域为
的定义域为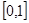 ,且
,且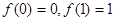 ,当
,当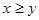 时,有
时,有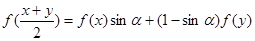 ,则使等式
,则使等式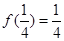 成立的
成立的 为第三象限,则
为第三象限,则 的值为 ( )
的值为 ( )