题目内容
已知
=(cos
+sin
,-sin
),
=(cos
-sin
,2cos
),设f(x)=
•
(1)求f(x)的最小正周期和单调递减区间;
(2)设关于x的方程f(x)=a在[-
,
]有两个不相等的实数根,求a的取值范围.
| AC |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| BC |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| AC |
| BC |
(1)求f(x)的最小正周期和单调递减区间;
(2)设关于x的方程f(x)=a在[-
| π |
| 2 |
| π |
| 2 |
(1)∵f(x)=
•
∴f(x)=(cos
+sin
)•(cos
-sin
)+(-sin
)•2cos
=cos(2×
)-sin(2×
)-2sin
cos
=cosx-sinx=
cos(x+
),
∴f(x)的最小正周期T=2π.
又由2kπ≤x+
≤π+2kπ,k∈Z,
∴-
+2kπ≤x≤
+2kπ,k∈Z.
故f(x)的单调递减区间是[-
+2kπ,
+2kπ](k∈Z).
(2)由f(x)=a,
∴
cos(x+
)=a,
∴cos(x+
)=
a,
又x∈[-
,
],
∴x+
∈[-
,
],数形结合得
≤
a<1
∴1≤a<
,
∴a的取值范围是[1,
).
| AC |
| BC |
∴f(x)=(cos
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=cos(2×
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=cosx-sinx=
| 2 |
| π |
| 4 |
∴f(x)的最小正周期T=2π.
又由2kπ≤x+
| π |
| 4 |
∴-
| π |
| 4 |
| 3π |
| 4 |
故f(x)的单调递减区间是[-
| π |
| 4 |
| 3π |
| 4 |
(2)由f(x)=a,
∴
| 2 |
| π |
| 4 |
∴cos(x+
| π |
| 4 |
| ||
| 2 |
又x∈[-
| π |
| 2 |
| π |
| 2 |
∴x+
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| ||
| 2 |
∴1≤a<
| 2 |
∴a的取值范围是[1,
| 2 |

练习册系列答案
相关题目
 且α为第二象限角,则m的允许值为 ;
且α为第二象限角,则m的允许值为 ; ,使
,使 ; ②函数
; ②函数 是偶函数;
是偶函数;  是函数
是函数 的一条对称轴的方程;
的一条对称轴的方程; 是第一象限的角,且
是第一象限的角,且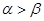 ,则
,则 .
.
