题目内容
设函数f(x)=sin(2x+
)+
sin2x-
cos2x.
(1)求f(x)的最小正周期及其图象的对称轴方程;
(2)将函数f(x)的图象向右平移
个单位长度,得到函数g(x)的图象,求g(x)在区间[-
,
]上的值域.
| π |
| 3 |
| ||
| 3 |
| ||
| 3 |
(1)求f(x)的最小正周期及其图象的对称轴方程;
(2)将函数f(x)的图象向右平移
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
f(x)=sin2xcos
+cos2xsin
-
cos2x
=
sin2x+
cos2x=
sin(2x+
),
(1)所以f(x)的最小正周期为T=π,
由2x+
=kπ+
,得x=
+
,k∈Z,
所以函数f(x)图象的对称轴方程为:x=
+
,k∈Z;
(2)由题意得,g(x)=f(x-
)=
sin(2x-
)=-
cos2x,
∵x∈[-
,
],∴2x∈[-
,
π],
从而cos2x∈[-
,1],
所以g(x)的值域为[-
,
].
| π |
| 3 |
| π |
| 3 |
| ||
| 3 |
=
| 1 |
| 2 |
| ||
| 6 |
| ||
| 3 |
| π |
| 6 |
(1)所以f(x)的最小正周期为T=π,
由2x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
所以函数f(x)图象的对称轴方程为:x=
| kπ |
| 2 |
| π |
| 6 |
(2)由题意得,g(x)=f(x-
| π |
| 3 |
| ||
| 3 |
| π |
| 2 |
| ||
| 3 |
∵x∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
从而cos2x∈[-
| 1 |
| 2 |
所以g(x)的值域为[-
| ||
| 3 |
| ||
| 6 |

练习册系列答案
相关题目
 且α为第二象限角,则m的允许值为 ;
且α为第二象限角,则m的允许值为 ; ,使
,使 ; ②函数
; ②函数 是偶函数;
是偶函数;  是函数
是函数 的一条对称轴的方程;
的一条对称轴的方程; 是第一象限的角,且
是第一象限的角,且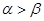 ,则
,则 .
. ,则
,则



