题目内容
已知向量
=(cos120°,sin120°),
=(cos30°,sin45°),则△ABC的形状为( )
| AB |
| BC |
| A.直角三角形 | B.等腰三角形 | C.锐角三角形 | D.钝角三角形 |
由题意可得:
•
=(cos120°,sin120°)•(cos30°,sin45°)
=(-
,
)•(
,
)=-
×
+
×
=
>0,
又向量的夹角<
,
>=π-B,故cos(π-B)>0,即cosB<0,故B为钝角,
故△ABC为钝角三角形
故选D
| AB |
| BC |
=(-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||||
| 4 |
又向量的夹角<
| AB |
| BC |
故△ABC为钝角三角形
故选D

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
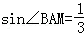 ,则sin∠BAC= _________ .
,则sin∠BAC= _________ .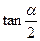 =2,求(1)
=2,求(1) 的值;(2)
的值;(2) 的值.
的值.