题目内容
先阅读下列不等式的证法,再解决后面的问题:已知 ,
, ,求证
,求证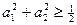 .
.
证明:构造函数 ,
,
因为对一切 ,恒有
,恒有 ≥0,所以
≥0,所以 ≤0,从而得
≤0,从而得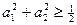 ,
,
(1)若 ,
, ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
 ,
, ,求证
,求证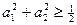 .
.证明:构造函数
 ,
,
因为对一切
 ,恒有
,恒有 ≥0,所以
≥0,所以 ≤0,从而得
≤0,从而得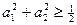 ,
,(1)若
 ,
, ,请写出上述结论的推广式;
,请写出上述结论的推广式;(2)参考上述解法,对你推广的结论加以证明.
见解析
(1)若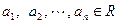 ,
, ,
,
 求证:
求证: ;……………………4分
;……………………4分
(2)证明:构造函数

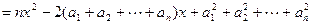
 ……………………
…………………… …8分
…8分
因 为对一切
为对一切 ,都有
,都有 ≥0,所以△=
≥0,所以△= ≤0,……10分
≤0,……10分
从而证得: .……12分
.……12分
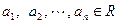 ,
, ,
, 求证:
求证: ;……………………4分
;……………………4分(2)证明:构造函数


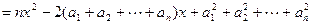
 ……………………
…………………… …8分
…8分
因
 为对一切
为对一切 ,都有
,都有 ≥0,所以△=
≥0,所以△= ≤0,……10分
≤0,……10分从而证得:
 .……12分
.……12分
练习册系列答案
相关题目
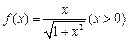 ,数列
,数列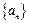 满足
满足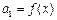 ,
,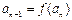 .
.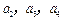 ;
; 五个方面的多元评价指标,并通过经验公式样
五个方面的多元评价指标,并通过经验公式样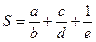 来计算各班的综合得分,S的值越高则评价效果越好,若某班在自测过程中各项指标显示出
来计算各班的综合得分,S的值越高则评价效果越好,若某班在自测过程中各项指标显示出 ,则下阶段要把其中一个指标的值增加1个单位,而使得S的值增加最多,那么该指标应为 .(填入
,则下阶段要把其中一个指标的值增加1个单位,而使得S的值增加最多,那么该指标应为 .(填入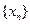 中,
中, ,且
,且 ,求出
,求出 并猜想通项公式
并猜想通项公式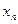 .
. 时,比较
时,比较 和
和 的大小并猜想( )
的大小并猜想( ) 时,
时,
 时,
时, 时,
时,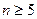 时,
时,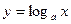 是减函数;已知
是减函数;已知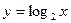 是对数函数,所以
是对数函数,所以 ,使得
,使得 能被
能被