题目内容
求函数f(x)="sinx+cosx+sinxcosx." x∈﹝0, ﹞的最大值并求出相应的x值.
﹞的最大值并求出相应的x值.
x= 。
。
解析试题分析:利用sinx与cosx的平方关系,令sinx+cosx=t,通过换元,将三角函数转化为二次函数,求出对称轴,利用二次函数的单调性求出最值.
设t=sinx+cosx=sin( +x),………(2分) x∈﹝0,
+x),………(2分) x∈﹝0,  ﹞
﹞
∴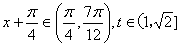 …………(5分)则
…………(5分)则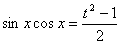
∴函数f(x)=sinx+cosx+sinxcosx=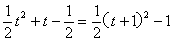 ……(8分)
……(8分)
∴函数f(x)在(1,)单调递增,∴当t=,t=sinx+cosx=sin( +x)时函数f(x)有最大值+
+x)时函数f(x)有最大值+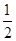 ……(10分)
……(10分)
此时,t=sinx+cosx=sin( +x)=,x=
+x)=,x= ……………(12分)..考点:同角三角函数的基本关系的运用;二次函数的性质的;换元法求三角函数的最值.
……………(12分)..考点:同角三角函数的基本关系的运用;二次函数的性质的;换元法求三角函数的最值.
点评:本小题主要是利用两角和公式的化简求值,二次函数的性质.此题是用换元法,转化思想.但要注意在换元时变量的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
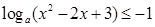 ,当
,当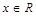 时恒成立.求
时恒成立.求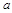 的取值范围.
的取值范围.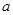 为非负实数,函数
为非负实数,函数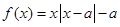 .
.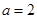 时,求函数的单调区间;
时,求函数的单调区间;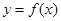 的零点个数,并求出零点.
的零点个数,并求出零点.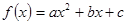 .
.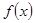 在
在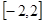 上的最大值、最小值分别是
上的最大值、最小值分别是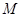 、
、 ,集合
,集合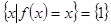 ,且
,且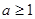 ,记
,记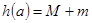 ,求
,求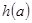 的最小值.
的最小值.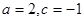 时,
时,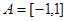 ,不等式
,不等式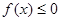 的解集为C,且
的解集为C,且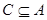 ,求实数
,求实数 的取值范围;
的取值范围;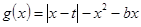
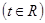 ,求
,求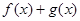 的最小值.
的最小值. 对于其定义域内的某一数
对于其定义域内的某一数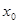 ,有
,有 ,则称
,则称 .
.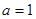 ,
,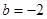 时,求函数
时,求函数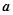 的取值范围;
的取值范围; 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数 的图象上,求实数b的最小值.
的图象上,求实数b的最小值.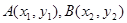 ,则线段AB的中点坐标为
,则线段AB的中点坐标为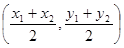 )
)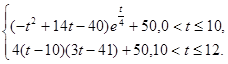
 .
.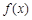 的定义域;(2)判断
的定义域;(2)判断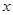 的不等式:
的不等式: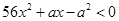
 中,设二次函数
中,设二次函数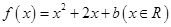 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为 .求:
.求: 的取值范围;
的取值范围;