题目内容
(本小题满分12分)
设平面直角坐标系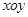 中,设二次函数
中,设二次函数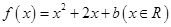 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为 .求:
.求:
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)求圆 的方程;
的方程;
(Ⅲ)问圆 是否经过某定点(其坐标与b 无关)?请证明你的结论.
是否经过某定点(其坐标与b 无关)?请证明你的结论.
(Ⅰ)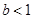 且
且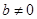
(Ⅱ)
(Ⅲ)见解析
解析试题分析:(Ⅰ)令 =0,得抛物线与
=0,得抛物线与 轴交点是
轴交点是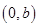 ;
;
令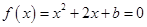 ,由题意
,由题意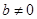 且Δ>0,
且Δ>0,
解得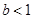 且
且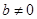 . ……2分
. ……2分
(Ⅱ)设所求圆的一般方程为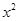
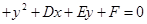 ,
,
令 =0 得
=0 得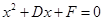 ,这与
,这与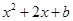 =0 是同一个方程,故
=0 是同一个方程,故
令 =0 得
=0 得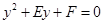 ,此方程有一个根为
,此方程有一个根为 ,代入得出
,代入得出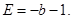
所以圆 的方程为
的方程为 . ……6分
. ……6分
(Ⅲ)圆 必过定点
必过定点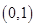 和
和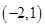 .
.
证明:法一:将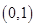 代入圆
代入圆 的方程,得左边=
的方程,得左边=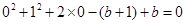 右边=
右边= ,
,
所以圆 必过定点
必过定点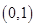 .
.
同理可证圆 必过定点
必过定点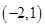 . ……12分
. ……12分
法二:圆 的方程为
的方程为 可化为
可化为
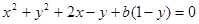
令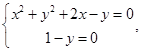 解得
解得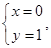 或
或
所以圆 必过定点
必过定点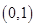 和
和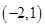 . ……12分
. ……12分
考点:本小题主要考查二次函数图象与性质、圆的方程的求法.
点评:由于圆的方程有两种形式:标准方程和一般方程,在做题时要合理选用,如果选择不恰当,可能会造成运算过于复杂而无法求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ﹞的最大值并求出相应的x值.
﹞的最大值并求出相应的x值.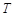 是时间
是时间 的函数:
的函数: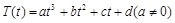 ,其中温度的单位是
,其中温度的单位是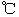 ,时间单位是小时,
,时间单位是小时,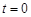 表示12:00,
表示12:00,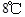 ,12:00的温度为
,12:00的温度为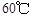 ,13:00的温度为
,13:00的温度为 ,且已知该物体的温度在8:00和16:00有相同的变化率.
,且已知该物体的温度在8:00和16:00有相同的变化率.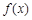 在区间
在区间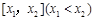 上的平均值为
上的平均值为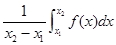 ,求该物体在8:00到16:00这段时间内的平均温度.
,求该物体在8:00到16:00这段时间内的平均温度.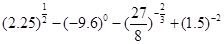 ;
;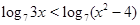 .
.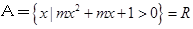 ,求实数
,求实数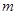 的取值范围;
的取值范围;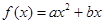 ,满足
,满足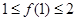 ,
,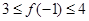 ,求
,求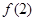 的取值范围.
的取值范围.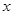 万元,每件产品的成本将降低
万元,每件产品的成本将降低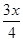 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)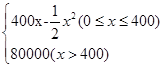 .
.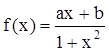 是定义在
是定义在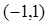 上的奇函数,且
上的奇函数,且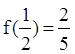
 的解析式。
的解析式。 在
在 上是增函数。
上是增函数。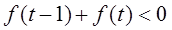
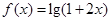 ,
, .
. 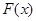 的定义域;
的定义域;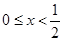 时,总有
时,总有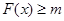 成立,求
成立,求 的取值范围.
的取值范围.