题目内容
(本小题满分10分)已知函数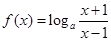 .
.
(1)求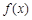 的定义域;(2)判断
的定义域;(2)判断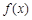 的奇偶性并证明;
的奇偶性并证明;
(1)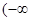 ,
,  ,
, 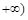 ;(2)见解析。
;(2)见解析。
解析试题分析:(1)∵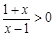 ∴
∴ 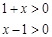 或
或 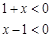 ,∴定义域为
,∴定义域为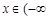 ,
,  ,
, 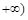 .---5分
.---5分
(2)由(1)知函数的定义域为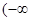 ,
,  ,
, 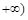 ,关于原点对称,
,关于原点对称,
又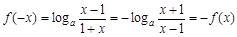 ,∴
,∴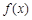 为奇函数.----10分
为奇函数.----10分
考点:本题考查函数定义域的求法;函数奇偶性的判断及证明;分式不等式的解法。
点评:在函数奇偶性的定义中,有两个必备条件:一是定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域对解决问题是有利的;二是判断f(x)与f(-x)是否具有等量关系.在判断奇偶性的运算中,可以转化判断奇偶性的等价等量关系式为f(x)+f(-x)=0(奇函数)或f(x)-f(-x)=0(偶函数)是否成立,这样能简化计算。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 个月内累计的需求量
个月内累计的需求量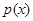 (百件)为
(百件)为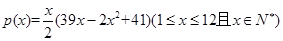
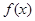 的表达式.
的表达式.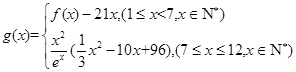 (单位:百件),每件利润
(单位:百件),每件利润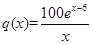 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少? 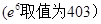
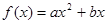 的图像过点
的图像过点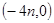 ,且
,且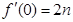 ,
,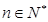
 的解析式;
的解析式; 满足
满足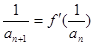 ,且
,且 ,求数列
,求数列 ,数列
,数列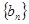 的前
的前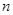 项和
项和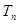 ,求证:
,求证: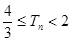 。
。 ﹞的最大值并求出相应的x值.
﹞的最大值并求出相应的x值.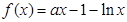
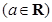 .
.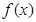 在定义域内的极值点的个数;
在定义域内的极值点的个数;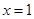 处取得极值,对
处取得极值,对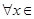
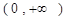 ,
,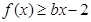 恒成立,求实数
恒成立,求实数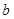 的取值范围;
的取值范围;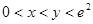 且
且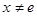 时,试比较
时,试比较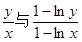 的大小.
的大小.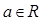 ,函数
,函数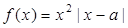 .
.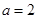 时,求使
时,求使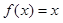 成立的
成立的 的集合;
的集合;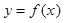 在区间
在区间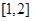 上的最小值.
上的最小值. 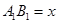 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于 的函数
的函数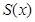 的解析式;
的解析式;
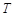 是时间
是时间 的函数:
的函数: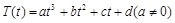 ,其中温度的单位是
,其中温度的单位是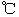 ,时间单位是小时,
,时间单位是小时,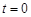 表示12:00,
表示12:00,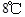 ,12:00的温度为
,12:00的温度为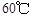 ,13:00的温度为
,13:00的温度为 ,且已知该物体的温度在8:00和16:00有相同的变化率.
,且已知该物体的温度在8:00和16:00有相同的变化率.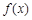 在区间
在区间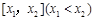 上的平均值为
上的平均值为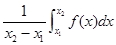 ,求该物体在8:00到16:00这段时间内的平均温度.
,求该物体在8:00到16:00这段时间内的平均温度.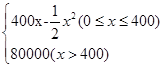 .
.