题目内容
定义:若函数 对于其定义域内的某一数
对于其定义域内的某一数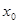 ,有
,有 ,则称
,则称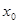 是
是 的一个不动点. 已知函数
的一个不动点. 已知函数 .
.
(1)当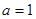 ,
,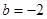 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意的实数b,函数 恒有两个不动点,求实数
恒有两个不动点,求实数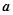 的取值范围;
的取值范围;
(3)在(2)的条件下,若 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数 的不动点,且线段AB的中点C在函数
的不动点,且线段AB的中点C在函数 的图象上,求实数b的最小值.
的图象上,求实数b的最小值.
(参考公式:若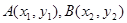 ,则线段AB的中点坐标为
,则线段AB的中点坐标为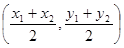 )
)
(1)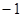 和3;(2)
和3;(2) ;(3)
;(3)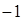 。
。
解析试题分析:(1) 当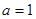 ,
,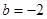 时
时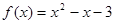 ,由
,由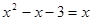 ,
,
解得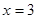 或
或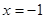 ,故所求的不动点为
,故所求的不动点为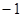 和3. ------------------3分
和3. ------------------3分
(2)令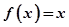 ,则
,则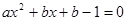 ①
①
由题意,方程①恒有两个不等实根,所以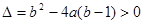 ------------5分
------------5分
即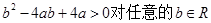 恒成立,
恒成立,
则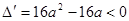 ,
, 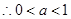 ------------------8分
------------------8分
(3)依题意设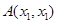 ,
,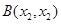
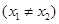 则AB中点C的坐标为
则AB中点C的坐标为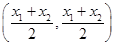
又AB的中点在直线 上
上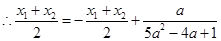 ∴
∴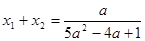 ------------9分
------------9分
又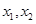 是方程①的两个根,
是方程①的两个根, 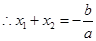 ,即
,即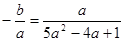 ,
,
∴ =
= =
=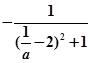 ------------11分
------------11分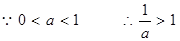
∴当 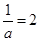
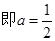 时,bmin=
时,bmin=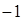 ------------------12分
------------------12分
考点:二次函数的性质。
点评:做此题的关键是:①理解新定义:求函数 的不动点即为求方程
的不动点即为求方程 =
=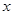 的根;②发现参数b可以表示成参数a的函数即
的根;②发现参数b可以表示成参数a的函数即 ,至此,求参数b最小值的问题转化为求b关于a的函数最小值的问题.
,至此,求参数b最小值的问题转化为求b关于a的函数最小值的问题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 的边际函数
的边际函数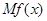 定义为
定义为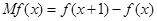 .某公司每月最多生产100台报警系统装置,生产
.某公司每月最多生产100台报警系统装置,生产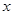 台(
台(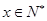 )的收入函数为
)的收入函数为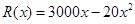 (单位:元),其成本函数为
(单位:元),其成本函数为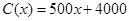 (单位:元),利润是收入与成本之差.
(单位:元),利润是收入与成本之差.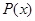 及边际利润函数
及边际利润函数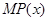 的解析式,并指出它们的定义域;
的解析式,并指出它们的定义域;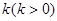 .现已知相距
.现已知相距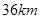 的
的 ,
, 两家化工厂(污染源)的污染强度分别为正数
两家化工厂(污染源)的污染强度分别为正数 ,
, ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数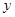 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设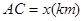 .
. 的函数;
的函数;  时,
时,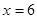 处取得最小值,试求
处取得最小值,试求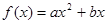 的图像过点
的图像过点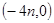 ,且
,且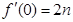 ,
,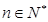
 的解析式;
的解析式; 满足
满足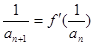 ,且
,且 ,求数列
,求数列 ,数列
,数列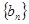 的前
的前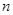 项和
项和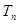 ,求证:
,求证: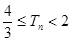 。
。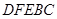 内修建一个矩形
内修建一个矩形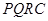 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且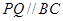 ,
,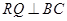 ,另外
,另外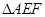 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量 ,
,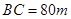 ,
, 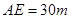 ,
,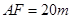 .
.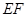 的方程;
的方程;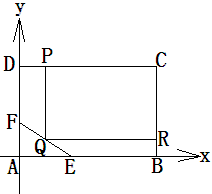
 ﹞的最大值并求出相应的x值.
﹞的最大值并求出相应的x值.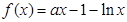
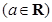 .
.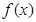 在定义域内的极值点的个数;
在定义域内的极值点的个数;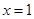 处取得极值,对
处取得极值,对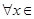
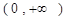 ,
,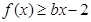 恒成立,求实数
恒成立,求实数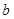 的取值范围;
的取值范围;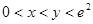 且
且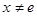 时,试比较
时,试比较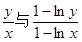 的大小.
的大小.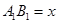 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于 的函数
的函数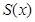 的解析式;
的解析式;
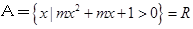 ,求实数
,求实数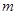 的取值范围;
的取值范围;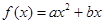 ,满足
,满足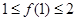 ,
,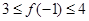 ,求
,求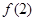 的取值范围.
的取值范围.