题目内容

19．定义运算a⊕b=a3-lnb，则函数f（x）=x⊕e2的图象大致为（　　）
A．B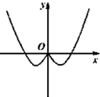．C．D．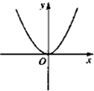

分析 由新定义得到函数的解析式，即可得到函数的图象．

解答 解：由a⊕b=a3-lnb，
∴f（x）=x⊕e2=x3-lne2=x3-2，
∴f′（x）=2x2≥0恒成立，
∴f（x）在R上单调递增，
故选：C．

点评 本题考查了函数的图象的识别和新定义的学习，属于基础题．

练习册系列答案
相关题目
9．设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与抛物线y2=8x有一个公共的焦点F，两曲线的一个交点为M．若|MF|=5，则椭圆的离心率为（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{1}{3}$D．$\frac{\sqrt{3}}{3}$
10．下列图象表示的函数中，不能用二分法求零点的是（　　）
A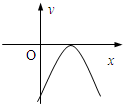．B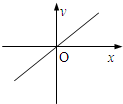．C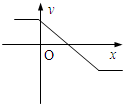．D．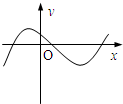
7．已知关于x的二次函数y=x2-2mx+m2+m的图象与关于x的函数y=kx+1的图象交于两点A（x1，y1）、B（x2，y2）（x1＜x2）；
（1）当k=1，m=0或1时，求AB的长；
（2）当k=1，m为任何值时，猜想AB的长是否不变？并证明你的猜想；
（3）当m=0，无论k为何值时，猜想△AOB的形状，并证明你的猜想．
（平面内两点间的距离公式AB=$\sqrt{（{x}_{1}-{x}_{2}）^{2}+（{y}_{1}-{y}_{2}）^{2}}$）．
14．对于定义在R上的函数f（x），若f（0）=1，且对任意的x∈R，都有f（x+1）-f（x）=2，则$\frac{2}{f（0）f（1）}$+$\frac{2}{f（1）f（2）}$+…+$\frac{2}{f（2014）f（2015）}$=$\frac{4030}{4031}$．
4．将八进制数123（8）化为十进制数，结果为83．
11．已知命题：
①将一组数据中的每个数都变为原来的2倍，则方差也变为原来的2倍；
②命题“?x∈R，x2+x+1＜0”的否定是“?x∈R，x2+x+1＜0”；
③在△ABC中，若A＞B，则sinA＜sinB；
④在正三棱锥S-ABC内任取一点P，使得VP-ABC＜$\frac{1}{2}$VS-ABC的概率是$\frac{7}{8}$；
⑤若对于任意的n∈N+，n2+（a-4）n+3+a≥0恒成立，则实数a的取值范围是[$\frac{1}{3}$，+∞）．
以上命题中正确的是③④⑤（填写所有正确命题的序号）．
8．函数$y=\frac{1}{2}cos2x$的周期为（　　）
A．πB．2πC．4πD．$\frac{π}{4}$
9．已知数列{an}的通项为an=log（n+1）（n+2）（n∈N*），我们把使乘积a1•a2•a3•…•an为整数的n叫做“优数”，则在（0，2015]内的所有“优数”的和为（　　）
A．1024B．2012C．2026D．2036

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网