题目内容
【题目】现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1 , y1)、B(x2 , y2)两点间的“直角距离”为:D(AB)=|x1﹣x2|+|y1﹣y2|. 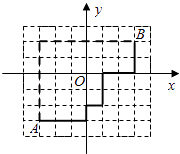
(1)在平面直角坐标系中,写出所有满足到原点的“直角距离”
为2的“格点”的坐标;(格点指横、纵坐标均为整数的点)
(2)定义:“圆”是所有到定点“直角距离”为定值的点组成的图形,点A(1,3),B(1,1),C(3,3),求经过这三个点确定的一个“圆”的方程,并画出大致图象;
(3)设P(x,y),集合B表示的是所有满足D(PO)≤1的点P所组成的集合,
点集A={(x,y)|﹣1≤x≤1,﹣1≤y≤1},
求集合Q={(x,y)|x=x1+x2 , y=y1+y2 , (x1 , y1)∈A,(x2 , y2)∈B}所表示的区域的面积.
【答案】
(1)解:0,2)、(1,1)、(2,0)、(1,﹣1)、(0,﹣2)、(﹣1,﹣1)、(﹣2,0)、(﹣1,1);
(2)解:设定点坐标为(a,b),定值为r,
则“圆”的方程为|x﹣a|+|y﹣b|=r.
则 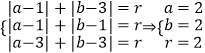 .
.
“圆”的方程为|x﹣2|+|y﹣2|=2.
作其图象如下,
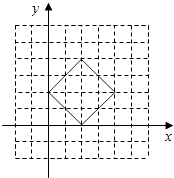 .
.
(3)解:B={(x,y)||x|+|y|≤1},
∵ ![]() ,
,
∴ ![]() ,
,
∵(x2,y2)∈B,
∴|x2|+|y2|≤1,
即|x﹣x1|+|y﹣y1|≤1,
∵点集A表示以原点为中心,边长为2的正方形及其内部,
∴点集Q表示以点A内的点为定点,1为定长的“圆”及其内部.
面积 ![]() .
.
【解析】(1)由题意可得|x|+|y|=2,从而写出格点即可;(2)设定点坐标为(a,b),定值为r,从而可得“圆”的方程为|x﹣a|+|y﹣b|=r,从而解得“圆”的方程为|x﹣2|+|y﹣2|=2,作其图象即可;(3)由题意,B={(x,y)||x|+|y|≤1},从而可得|x﹣x1|+|y﹣y1|≤1,从而可得点集Q表示以点A内的点为定点,1为定长的“圆”及其内部,从而求面积.