题目内容
【题目】在区间D上,如果函数f(x)为减函数,而xf(x)为增函数,则称f(x)为D上的弱减函数.若f(x)= ![]()
(1)判断f(x)在区间[0,+∞)上是否为弱减函数;
(2)当x∈[1,3]时,不等式 ![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数g(x)=f(x)+k|x|﹣1在[0,3]上有两个不同的零点,求实数k的取值范围.
【答案】
(1)解:由初等函数性质知, ![]() 在[0,+∞)上单调递减,
在[0,+∞)上单调递减,
而 ![]() 在[0,+∞)上单调递增,
在[0,+∞)上单调递增,
所以 ![]() 是[0,+∞)上的弱减函数.
是[0,+∞)上的弱减函数.
(2)解:不等式化为 ![]() 在x∈[1,3]上恒成立,则
在x∈[1,3]上恒成立,则 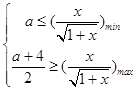 ,
,
而 ![]() 在[1,3]单调递增,∴
在[1,3]单调递增,∴ ![]() 的最小值为
的最小值为 ![]() ,
, ![]() 的最大值为
的最大值为 ![]() ,
,
∴ 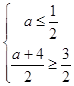 ,∴a∈[﹣1,
,∴a∈[﹣1, ![]() ].
].
(3)解:由题意知方程 ![]() 在[0,3]上有两个不同根,
在[0,3]上有两个不同根,
①当x=0时,上式恒成立;
②当x∈(0,3]时,则由题意可得方程 ![]() 只有一解,
只有一解,
根据 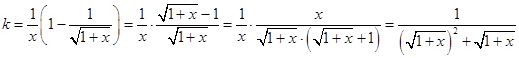 ,
,
令 ![]() ,则t∈(1,2],
,则t∈(1,2],
方程化为 ![]() 在t∈(1,2]上只有一解,所以
在t∈(1,2]上只有一解,所以 ![]() .
.
【解析】(1)利用初等函数的性质、弱减函数的定义,判断 ![]() 是[0,+∞)上的弱减函数.(2)根据题意可得
是[0,+∞)上的弱减函数.(2)根据题意可得 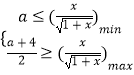 ,再利用函数的单调性求得函数的最值,可得a的范围.(3)根据题意,当x∈(0,3]时,方程
,再利用函数的单调性求得函数的最值,可得a的范围.(3)根据题意,当x∈(0,3]时,方程 ![]() 只有一解,分离参数k,换元利用二次函数的性质,求得k的范围.
只有一解,分离参数k,换元利用二次函数的性质,求得k的范围.
【考点精析】关于本题考查的函数单调性的性质,需要了解函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能得出正确答案.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】北京市为了缓解交通压力,计划在某路段实施“交通限行”,为调查公众对该路段“交通限行”的态度,某机构从经过该路段的人员中随机抽查了80人进行调查,将调查情况进行整理,制成表:
年龄(岁) | [15,30) | [30,45) | [45,60) | [60,75) |
人数 | 24 | 26 | 16 | 14 |
赞成人数 | 12 | 14 | x | 3 |
(1)若经过该路段的人员对“交通限行”的赞成率为0.40,求x的值;
(2)在(1)的条件下,若从年龄在[45,60),[60,75)内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自[60,75)内的概率.