题目内容
【题目】如图，有一块半径为2的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径，上底CD的端点在圆周上．设∠DAB=θ（0＜θ＜ 
），L为等腰梯形ABCD的周长． 
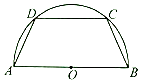
（1）求周长L与θ的函数解析式；
（2）试问周长L是否存在最大值？若存在，请求出最大值，并指出此时θ的大小；若不存在，请说明理由．
【答案】
（1）解：连接BD，则∠ADB=90°，
∴AD=BC=4cosθ．
作DE⊥AB于M，CN⊥AB于N，
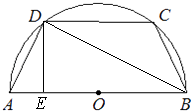
得AM=BN=ADcosθ=4cos2θ，
∴DC=AB﹣2AM=4﹣8cos2θ．
∴△ABC的周长L=AB+2AD+DC=4+8cosθ+（4﹣8cos2θ）=8+8cosθ﹣8cos2θ．
（2）解：令t=cosθ，由 
，知t∈（0，1）．
则 
，
当t= 
，即 
， 
时，L有最大值10．
∴当θ=60°时，L存在最大值10
【解析】（1）由于AB是圆O的直径，所以三角形ABD是直角三角形，连BD，过D作DE⊥AB于E，则由射影定理可知AD2=AEAB，从而可用腰长表示上底长，进而可求梯形的周长y与腰长x之间的函数关系式，根据上底长，可确定函数的定义域；（2）令t=cosθ，由 
，知t∈（0，1）．利用配方法可知函数函数在（0， 
）上单调递增，在（ ，1）单调递减，由此可求周长y的最大值．
【题目】北京市为了缓解交通压力，计划在某路段实施“交通限行”，为调查公众对该路段“交通限行”的态度，某机构从经过该路段的人员中随机抽查了80人进行调查，将调查情况进行整理，制成表：
年龄（岁） | [15，30） | [30，45） | [45，60） | [60，75） |
人数 | 24 | 26 | 16 | 14 |
赞成人数 | 12 | 14 | x | 3 |
（1）若经过该路段的人员对“交通限行”的赞成率为0.40，求x的值；
（2）在（1）的条件下，若从年龄在[45，60），[60，75）内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访，求选中的2人中至少有1人来自[60，75）内的概率．
