题目内容
【题目】综合题
（1）解不等式：3≤x2﹣2x＜8；
（2）已知a，b，c，d均为实数，求证：（a2+b2）（c2+d2）≥（ac+bd）2 ．
【答案】
（1）解：不等式：3≤x2﹣2x＜8，
即：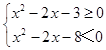 
，解得： 
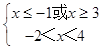，即x∈（﹣2，﹣1]∪[3，4）．
（2）证明：∵（a2+b2）（c2+d2）﹣（ac+bd）2
=a2c2+a2d2+b2c2+b2d2﹣a2c2﹣2abcd﹣b2d2
=a2d2+b2c2﹣2abcd
=（ad﹣bc）2≥0
∴（a2+b2）（c2+d2）≥（ac+bd）2．
【解析】（1）直接利用二次不等式化简求解即可．（2）利用作差法化简，证明即可．
【考点精析】解答此题的关键在于理解不等式的证明的相关知识，掌握不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】北京市为了缓解交通压力，计划在某路段实施“交通限行”，为调查公众对该路段“交通限行”的态度，某机构从经过该路段的人员中随机抽查了80人进行调查，将调查情况进行整理，制成表：
年龄（岁） | [15，30） | [30，45） | [45，60） | [60，75） |
人数 | 24 | 26 | 16 | 14 |
赞成人数 | 12 | 14 | x | 3 |
（1）若经过该路段的人员对“交通限行”的赞成率为0.40，求x的值；
（2）在（1）的条件下，若从年龄在[45，60），[60，75）内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访，求选中的2人中至少有1人来自[60，75）内的概率．
