Question

【题目】已知函数f（x）=x+xlnx，若k∈Z，且k（x﹣1）＜f（x）对任意的x＞1恒成立，则k的最大值为（ ）
A.2
B.3
C.4
D.5

Answer 1

【答案】B
【解析】解：由k（x﹣1）＜f（x）对任意的x＞1恒成立， 得：k＜ ，（x＞1），
令h（x）= ，（x＞1），则h′（x）= ，
令g（x）=x﹣lnx﹣2=0，得：x﹣2=lnx，
画出函数y=x﹣2，y=lnx的图象，如图示：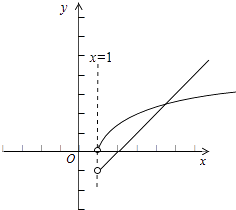

∴g（x）存在唯一的零点，
又g（3）=1﹣ln3＜0，g（4）=2﹣ln4=2（1﹣ln2）＞0，
∴零点属于（3，4）；
∴h（x）在（1，x0）递减，在（x0 ， +∞）递增，
而3＜h（3）= ＜4， ＜h（4）= ＜4，
∴h（x0）＜4，k∈Z，
∴k的最大值是3．
故选：B．