题目内容
7.在矩形ABCD中,点M在线段BC上,点N在线段CD上.且AB=4.AD=2,MN=$\sqrt{5}$,则$\overrightarrow{AM}$$•\overrightarrow{AN}$的最小值是( )| A. | 8 | B. | 10 | C. | 12 | D. | 15 |
分析 先以$\overrightarrow{AB}$所在的直线为x轴,以$\overrightarrow{AD}$所在的直线为x轴,建立坐标系,写出要用的点的坐标,根据两个点的位置得到坐标之间的关系,表示出两个向量的数量积,根据MN=$\sqrt{5}$,再由三角换元,结合辅助角公式和正弦函数的值域,即要求得数量积的最小值.
解答 解:以$\overrightarrow{AB}$所在的直线为x轴,以$\overrightarrow{AD}$所在的直线为x轴,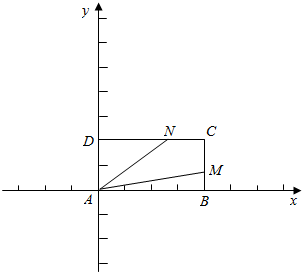
建立坐标系如图,
∵AB=4,AD=2,
∴A(0,0),B(4,0),C(4,2),
D(0,2),
设M(4,b),N(c,2),
由MN=$\sqrt{5}$,可得(b-2)2+(c-4)2=5,
又$\overrightarrow{AM}$•$\overrightarrow{AN}$=2b+4c,
可令b=2+$\sqrt{5}$cosθ,c=4+$\sqrt{5}$sinθ,
即有2b+4c=20+2$\sqrt{5}$cosθ+4$\sqrt{5}$sinθ
=20+10sin(θ+α),
当sin(θ+α)=-1时,取得最小值,且为10.
故选:B.
点评 本题考查向量的数量积的坐标运算,考查数形结合的思想方法,以及三角换元和正弦函数的值域的运用,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
18.已知函数f(x)=$\left\{\begin{array}{l}{1,x≤1}\\{-1,x>1}\end{array}\right.$则不等式xf(x+1)<x2-2的解集为( )
| A. | (-1,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1) | D. | (1,+∞) |