题目内容
15.已知f(x)=x2-4x+3在[0,a]的值域是[-1,3].实数a的取值范围记为集合A,g(x)=cos2x+$\frac{a}{2}$sinx.记g(x)的最大值为g(a).若g(a)≥b,对任意实数a∈A恒成立,则实数b的取值范围是b≤$\frac{5}{4}$.分析 作函数f(x)=x2-4x+3的图象,从而可得A=[2,4];再化简g(x)=-(sinx-$\frac{a}{4}$)2+1+$\frac{{a}^{2}}{16}$,从而可得g(a)=1+$\frac{{a}^{2}}{16}$,再求g(a)的最小值即可.
解答 解:作函数f(x)=x2-4x+3的图象如下,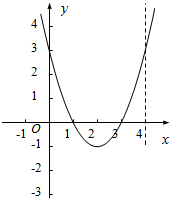 ,
,
∵f(x)=x2-4x+3在[0,a]的值域是[-1,3],
∴2≤a≤4,故A=[2,4];
g(x)=cos2x+$\frac{a}{2}$sinx=1-sin2x+$\frac{a}{2}$sinx
=-(sinx-$\frac{a}{4}$)2+1+$\frac{{a}^{2}}{16}$,
∵$\frac{1}{2}$≤$\frac{a}{4}$≤1,
∴g(a)=1+$\frac{{a}^{2}}{16}$,
∵A=[2,4],∴gmin(a)=1+$\frac{1}{4}$=$\frac{5}{4}$,
∵g(a)≥b对任意实数a∈A恒成立,
∴b≤$\frac{5}{4}$,
故答案为:b≤$\frac{5}{4}$.
点评 本题考查了二次函数的性质与应用,三角函数的最值的求法,同时考查了恒成立问题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目