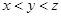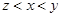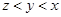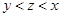题目内容
设函数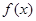 的定义域为
的定义域为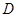 ,如果存在正实数
,如果存在正实数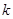 ,对于任意
,对于任意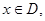 都有
都有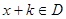 ,且
,且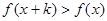 恒成立,则称函数
恒成立,则称函数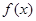 为
为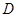 上的“
上的“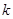 型增函数”。已知函数
型增函数”。已知函数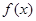 是定义在
是定义在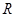 上的奇函数,且当
上的奇函数,且当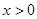 时,
时,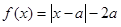 ,若
,若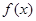 为
为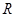 上的“
上的“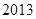 型增函数”,则实数
型增函数”,则实数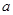 的取值范围是 .
的取值范围是 .
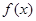 的定义域为
的定义域为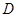 ,如果存在正实数
,如果存在正实数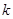 ,对于任意
,对于任意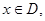 都有
都有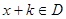 ,且
,且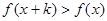 恒成立,则称函数
恒成立,则称函数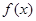 为
为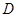 上的“
上的“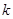 型增函数”。已知函数
型增函数”。已知函数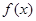 是定义在
是定义在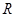 上的奇函数,且当
上的奇函数,且当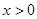 时,
时,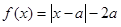 ,若
,若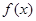 为
为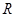 上的“
上的“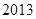 型增函数”,则实数
型增函数”,则实数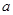 的取值范围是 .
的取值范围是 .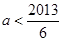
试题分析:
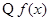 是定义在
是定义在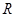 上的奇函数,且当
上的奇函数,且当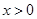 时,
时,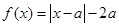 ,
,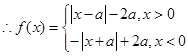
又
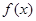 为
为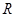 上的”
上的”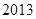 型增函数”,
型增函数”,当
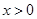 时,由定义有
时,由定义有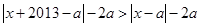 ,即
,即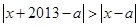 ,其几何意义为到点
,其几何意义为到点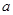 小于到点
小于到点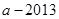 的距离,由于
的距离,由于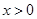 故可知
故可知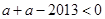 得
得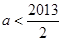 ,
,当
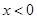 时,分两类研究,若
时,分两类研究,若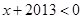 ,则有
,则有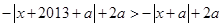 ,即
,即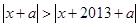 ,其几何意义表示到点
,其几何意义表示到点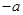 的距离小于到点
的距离小于到点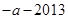 的距离,由于
的距离,由于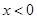 ,故可得
,故可得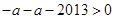 ,得
,得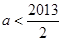 ;若
;若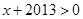 ,则有
,则有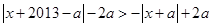 ,即
,即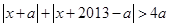 ,其几何意义表示到点
,其几何意义表示到点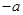 的距离与到点
的距离与到点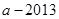 的距离和大于
的距离和大于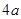 ,当
,当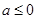 时,显然成立,当
时,显然成立,当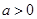 时,由于
时,由于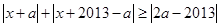 ,故有
,故有 ,必有
,必有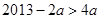 .解得
.解得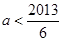 .
.故答案:
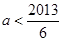

练习册系列答案
相关题目
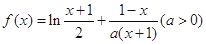 .
.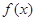 在
在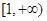 上为增函数, 求实数
上为增函数, 求实数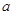 的取值范围;
的取值范围;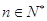 且
且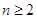 时,
时,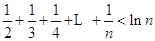 .
. 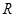 上的函数
上的函数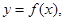 当
当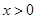 时,
时,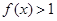 ,且对任意的
,且对任意的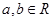 有
有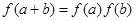 。
。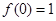 ,
,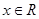 ,恒有
,恒有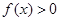 ;
;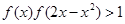 ,求
,求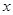 的取值范围。
的取值范围。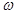 >0,若函数
>0,若函数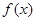 =sin
=sin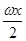 cos
cos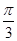 ,
,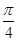 ]上单调递增,则
]上单调递增,则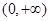 上为增函数的是
上为增函数的是



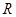 上的偶函数
上的偶函数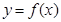 满足:
满足: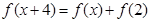 ,且当
,且当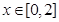 时,
时,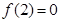 ;
;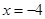 为函数
为函数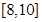 单调递增;
单调递增;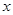 的方程
的方程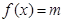 在
在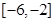 上的两根
上的两根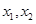 ,则
,则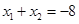 .
.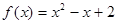 ,则下列关系中一定正确的是
,则下列关系中一定正确的是 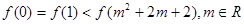
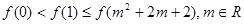
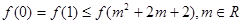
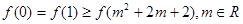
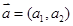 ,
,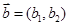 ,定义一运算:
,定义一运算: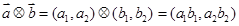 ,已知
,已知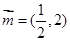 ,
,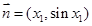 .点Q在
.点Q在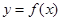 的图像上运动,且满足
的图像上运动,且满足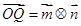 (其中O为坐标原点),则
(其中O为坐标原点),则


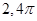
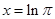 ,
,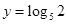 ,
,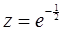 ,则
,则