题目内容
【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
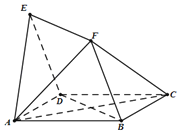
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(Ⅰ)设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,因为四边形
,因为四边形![]() 为菱形,所以
为菱形,所以![]() ,且
,且![]() 为
为![]() 中点,由
中点,由![]() ,知
,知![]() ,由此能够证明
,由此能够证明![]() 平面
平面![]() ;(Ⅱ)因为四边形
;(Ⅱ)因为四边形![]() 与
与![]() 均为菱形,所以
均为菱形,所以![]() ,平面
,平面![]() 平面
平面![]() ,由此能够证明
,由此能够证明![]() 平面
平面![]() ;(Ⅲ)因为四边形
;(Ⅲ)因为四边形![]() 为菱形,且
为菱形,且![]() ,所以
,所以![]() 为等边三角形,因为
为等边三角形,因为![]() 为
为![]() 中点,所以
中点,所以![]() ,故
,故![]() 平面
平面![]() ,由
,由![]() 两两垂直,建立空间直角坐标系
两两垂直,建立空间直角坐标系![]() ,设
,设![]() ,因为四边形
,因为四边形![]() 为菱形,
为菱形, ![]() ,则
,则![]() ,所以
,所以![]() ,
, ![]() ,求得平面
,求得平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,由此能求出二面角
,由此能求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)证明:设AC与BD相交于点O,
连接FO.因为四边形ABCD为菱形,所以AC⊥BD,且O为AC中点.
又 FA=FC,所以 AC⊥FO.
因为 FO∩BD=O,
所以 AC⊥平面BDEF.
(Ⅱ)证明:因为四边形ABCD与BDEF均为菱形,
所以AD∥BC,DE∥BF,
所以 平面FBC∥平面EAD.
又FC平面FBC,所以FC∥平面EAD.
(Ⅲ)解:因为四边形BDEF为菱形,且∠DBF=60°,
所以△DBF为等边三角形.
因为O为BD中点,所以FO⊥BD,故FO⊥平面ABCD.
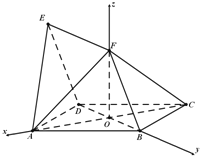
由OA,OB,OF两两垂直,建立如图所示的空间直角坐标系O﹣xyz. …(9分)
设AB=2.因为四边形ABCD为菱形,∠DAB=60°,
则BD=2,所以OB=1,![]() .所以
.所以 ![]() .
.
所以 ![]() ,
,![]() .
.
设平面BFC的法向量为![]() =(x,y,z),
=(x,y,z),
则有![]() ,
,
取x=1,得![]() .
.
∵平面AFC的法向量为![]() =(0,1,0).
=(0,1,0).
由二面角A﹣FC﹣B是锐角,得|cos<![]() ,
,![]() >|=
>|=![]() =
=![]() .
.
所以二面角A﹣FC﹣B的余弦值为![]() .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50 名,其中每天玩微信超过6 小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有60%的把握认为“微信控”与”性别“有关?
(2)现从调查的女性用户中按分层抽样的方法选出5 人并从选出的5 人中再随机抽取3 人赠送200 元的护肤品套装,记这3 人中“微信控”的人数为X,试求X 的分布列与数学期望.
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出![]() 次成功交易,并对其评价进行统计爱,商品和服务评价的
次成功交易,并对其评价进行统计爱,商品和服务评价的![]() 列联表如下表:
列联表如下表:
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 |
|
|
|
对商品不满意 |
|
|
|
合计 |
|
|
|
(1)是否可以在犯错误概率不超过![]() 的前提下,认为商品好评与服务好评有关?
的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的![]() 次购物中,设对商品和服务全好评的次数为随机变量
次购物中,设对商品和服务全好评的次数为随机变量![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(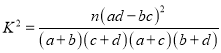 ,其中
,其中![]() )
)
