Question

【题目】已知椭圆 (a>b>0)的左、右焦点分别为F1，F2，点M(0，2)是椭圆的一个顶点，△F1MF2是等腰直角三角形．

(1)求椭圆的方程；

(2)过点M分别作直线MA，MB交椭圆于A，B两点，设两直线的斜率分别为k1，k2，且k1＋k2＝8，证明：直线AB过定点.

Answer 1

【答案】(1) ;(2)见解析.

【解析】试题分析：

(1)由题意求得，则椭圆的方程为;

(2)分类讨论直线的斜率不存在和直线斜率存在两种情况即可证得直线AB过定点.

试题解析：

(1)因为b＝2，△F1MF2是等腰直角三角形，所以c＝2，所以a＝2，

故椭圆的方程为＋＝1.

(2)证明：①若直线AB的斜率存在，设直线AB的方程为y＝kx＋m，

A点坐标为(x1，y1)，B点坐标为(x2，y2)，联立方程得，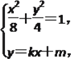

消去y，得(1＋2k2)x2＋4kmx＋2m2－8＝0，

则x1＋x2＝－，x1x2＝.

由题知k1＋k2＝＋＝8，

所以＋＝8，即2k＋(m－2)＝8.

所以k－＝4，整理得m＝k－2.

故直线AB的方程为y＝kx＋k－2，即y＝k－2。

所以直线AB过定点.

②若直线AB的斜率不存在，设直线AB的方程为x＝x0，A(x0，y0)，

B(x0，－y0)，则由题知＋＝8，

得x0＝－.此时直线AB的方程为x＝－，

显然直线AB过点.

综上可知，直线AB过定点.