题目内容
【题目】已知f（x）=x2+bx+c（b，c∈R，b＜0）．
（1）若f（x）的定义域为[0，1]时，值域也是[0，1]，求b，c的值；
（2）若b=﹣2时，若函数g（x）= 
对任意x∈[3，5]，g（x）＞c恒成立，试求实数c的取值范围．
【答案】
（1）解：二次函数f（x）=x2+bx+c的对称轴是x=﹣ 
，开口向上
①当0＜﹣ ≤ 
，即﹣1≤b＜0
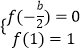解得b=﹣4，c=4，不合题意；
②当 
，即﹣2＜b＜﹣1；
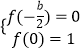解得b=﹣2，c=1，不符合，舍去．
③当﹣ 
，即b≤2 
解得b=﹣2，c=1，符合．
∴b=﹣2，c=1
（2）解：若b=﹣2时，若函数g（x）= 
对任意x∈[3，5]，g（x）＞c恒成立，
即 
对x∈[3，5]恒成立，
即x2﹣（2+c）x+c＞0对x∈[3，5]恒成立．
即c＜ 
对x∈[3，5]恒成立，c＜（x﹣1）﹣ 
令h（x）=（x﹣1）﹣ ，h（x）在x∈[3，5]为单调递增函数
∴h（x）min=h（3）= 
∴c＜
【解析】（1）讨论对称轴x=﹣ 在区间[0，1]的位置关系，列出等式，解出a，b；（2）若b=﹣2时，若函数g（x）= 对任意x∈[3，5]，g（x）＞c恒成立，即可转化为：即c＜ 对x∈[3，5]恒成立．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减才能正确解答此题．
【题目】已知f（x）=loga 
是奇函数（其中a＞1）
（1）求m的值；
（2）判断f（x）在（2，+∞）上的单调性并证明；
（3）当x∈（r，a﹣2）时，f（x）的取值范围恰为（1，+∞），求a与r的值．
【题目】设函数f（x）=lg[log 
（ 
x﹣1）]的定义域为集合A，集合B={x|x＜1，或x≥3}．
（1）求A∪B，（RB）∩A；
（2）若2a∈A，且log2（2a﹣1）∈B，求实数a的取值范围．
【题目】某课题组对春晚参加“咻一咻”抢红包活动的同学进行调查，按照使用手机系统不同（安卓系统和IOS系统）分别随机抽取5名同学进行问卷调查，发现他们咻得红包总金额数如表所示：
手机系统 | 一 | 二 | 三 | 四 | 五 |
安卓系统（元） | 2 | 5 | 3 | 20 | 9 |
IOS系统（元） | 4 | 3 | 18 | 9 | 7 |
（1）如果认为“咻”得红包总金额超过6元为“咻得多”，否则为“咻得少”，请判断手机系统与咻得红包总金额的多少是否有关？
（2）要从5名使用安卓系统的同学中随机选出2名参加一项活动，以X表示选中的同学中咻得红包总金额超过6元的人数，求随机变量X的分布列及数学期望E（X）．
下面的临界值表供参考：
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
独立性检验统计量 
，其中n=a+b+c+d．
