题目内容
【题目】已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过焦点垂直长轴的弦长为3.
,过焦点垂直长轴的弦长为3.
(1)求椭圆的标准方程;
(2)过椭圆的右顶点作直线交抛物线y2=2x于A、B两点,求证:OA⊥OB.
【答案】
(1)解:椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过焦点垂直长轴的弦长为3,
,过焦点垂直长轴的弦长为3,
则有 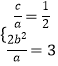 ,
,
解可得a=2,c=1,则b2=a2﹣c2=3.
所以,所求椭圆的标准方程为 ![]()
(2)解:证明:设过椭圆的右顶点(2,0)的直线AB的方程为x=my+2.
代入抛物线方程y2=2x,得y2﹣2my﹣4=0.
设A(x1,y1)、B(x2,y2),
则 ![]() ,
,
∴x1x2+y1y2=(my1+2)(my2+2)+y1y2=(1+m2)y1y2+2m(y1+y2)+4=0.
∴OA⊥OB
【解析】(1)根据题意,分析可得 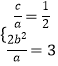 ,解可得a、c的值,由椭圆的定义可得b的值,将a、b的值代入椭圆方程即可得答案;(2)设过椭圆的右顶点(2,0)的直线AB的方程为x=my+2,与抛物线方程联立,设出A、B点的坐标,由根与系数的关系的关系分析计算x1x2+y1y2的值,由向量数量积的性质可得证明.
,解可得a、c的值,由椭圆的定义可得b的值,将a、b的值代入椭圆方程即可得答案;(2)设过椭圆的右顶点(2,0)的直线AB的方程为x=my+2,与抛物线方程联立,设出A、B点的坐标,由根与系数的关系的关系分析计算x1x2+y1y2的值,由向量数量积的性质可得证明.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目