Question

【题目】如图，四棱锥P－ABCD中，PA⊥底面ABCD ， AD∥BC ， AB＝AD＝AC＝3，PA＝BC＝4，M为线段AD上一点，AM＝2MD ， N为PC的中点．

（1）证明MN∥平面PAB；
（2）求四面体N－BCM的体积．

Answer 1

【答案】
（1）证明：由已知得AM＝ AD＝2，如图，

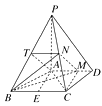
取BP的中点T，连接AT，TN，由N为PC中点知TN∥BC，TN＝ BC＝2.又AD∥BC，故 ，所以四边形AMNT为平行四边形，

于是MN∥AT.因为AT平面PAB，MN平面PAB，所以MN∥平面PAB

（2）解：因为PA⊥平面ABCD，N为PC的中点，所以N到平面ABCD的距离为 PA.

如图，取BC的中点E，连接AE，由AB＝AC＝3得AE⊥BC，AE＝ ＝ .

由AM∥BC得M到BC的距离为 ，故S△BCM＝ ×4× ＝2 ，

所以四面体N－BCM的体积VN－BCM＝ ×S△BCM× ＝ .

【解析】1.本题考察直线与平面平行的判定及直线与平面平行的性质，由线线平行证线面平行。2.求四面体N－BCM的体积=底面积高，要想到“PA⊥平面ABCD”的作用，结合题目的已知即可解出。