��Ŀ����
����Ŀ���������һ����װ�У���ͼ��ʾ��ABCD�DZ߳�Ϊ60cm��������ӲֽƬ����ȥ��Ӱ������ʾ���ĸ�ȫ�ȵĵ���ֱ�������Σ�������������ʹ��A��B��C��D�ĸ����غ���ͼ�еĵ�P�������γ�һ������������״�İ�װ�У�E��F��AB�ϣ��DZ���ȥ�ĵ���ֱ��������б�ߵ������˵㣬��AE=FB=x��cm���� 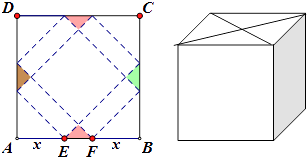
��1���������Ҫ���װ�в����S��cm2���������xӦȡ��ֵ��
��2���������Ҫ���װ���ݻ�V��cm3���������xӦȡ��ֵ���������ʱ��װ�еĸ������߳��ı�ֵ��
���𰸡�
��1���⣺���װ�еĸ�Ϊh��cm��������߳�Ϊa��cm������a= ![]() x��h=
x��h= ![]() ��30��x����0��x��30��
��30��x����0��x��30��
S=4ah=8x��30��x��=��8��x��15��2+1800��
�൱x=15ʱ��Sȡ���ֵ
��2���⣺V=a2h=2 ![]() ����x3+30x2����V��=6
����x3+30x2����V��=6 ![]() x��20��x����
x��20��x����
��V��=0��x=20��
��x�ʣ�0��20��ʱ��V�䣾0����x�ʣ�20��30��ʱ��V�䣼0��
�൱x=20ʱ����װ���ݻ�V��cm3�����
��ʱ�� ![]() ��
��
����ʱ��װ�еĸ������߳��ı�ֵ�� ![]()
����������1�������װ�еĸ�Ϊh��cm��������߳�Ϊa��cm����д��a��h��x�Ĺ�ϵʽ����ע��x��ȡֵ��Χ�������ò������ʽ��ʾ����װ�в����S����x�ĺ�������ʽ����������ʱ��ȡ�����ֵ���ɣ���2�����������ʽ��ʾ����װ���ݻ�V����x�ĺ�������ʽ��������õ���֪ʶ�����ʱ��ȡ�õ����ֵ���ɣ�