题目内容
【题目】如图,在三棱锥S﹣ABC中,M、N分别是棱SC、BC的中点,且MN⊥AM,若AB=2 ![]() ,则此正三棱锥外接球的体积是( )
,则此正三棱锥外接球的体积是( )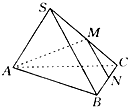
A.12π
B.4 ![]() π
π
C.![]() π
π
D.12 ![]() π
π
【答案】B
【解析】解:∵三棱锥S﹣ABC正棱锥,∴SB⊥AC(对棱互相垂直)∴MN⊥AC
又∵MN⊥AM而AM∩AC=A,∴MN⊥平面SAC即SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球.
∴侧棱长为:2,
∴R= ![]() ,
,
∴正三棱锥外接球的体积是 ![]() =
= ![]() .
.
所以答案是:B.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

练习册系列答案
相关题目