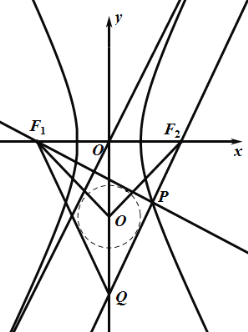
题目内容
【题目】已知![]() ,
,![]() 分别是双曲线
分别是双曲线![]() 的左,右焦点,过点
的左,右焦点,过点![]() 向一条渐近线作垂线,交双曲线右支于点
向一条渐近线作垂线,交双曲线右支于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() (
(![]() ,
,![]() 在
在![]() 轴同侧),连接
轴同侧),连接![]() ,若
,若![]() 的内切圆圆心恰好落在以
的内切圆圆心恰好落在以![]() 为直径的圆上,则
为直径的圆上,则![]() 的大小为________;双曲线的离心率为________.
的大小为________;双曲线的离心率为________.
【答案】![]()
![]()
【解析】
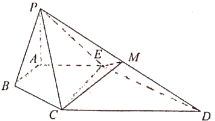
如图所示:不妨取渐近线![]() ,易知
,易知![]() ,设内切圆圆心为
,设内切圆圆心为![]() ,根据对称性知
,根据对称性知![]() 在
在![]() 轴上,得到
轴上,得到![]() ,根据距离相等得到直线
,根据距离相等得到直线![]() :
:![]() ,联立方程得到
,联立方程得到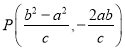 ,代入双曲线方程,计算得到答案.
,代入双曲线方程,计算得到答案.
如图所示:不妨取渐近线![]() ,易知
,易知![]() ,(否则不能与右支相交).
,(否则不能与右支相交).
则直线![]() 为:
为:![]() ,即
,即![]() ,
,
设内切圆圆心为![]() ,根据对称性知
,根据对称性知![]() 在
在![]() 轴上,
轴上,
![]() 的内切圆圆心恰好落在以
的内切圆圆心恰好落在以![]() 为直径的圆上,故
为直径的圆上,故![]() ,故
,故![]() ,
,
![]() 到直线
到直线![]() 的距离为:
的距离为:![]() ,
,
设直线![]() :
:![]() ,即
,即![]()
![]() 到直线
到直线![]() 的距离为:
的距离为:![]() ,
,
化简整理得到![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,直线
时,直线![]() 与
与![]() 的交点横坐标为
的交点横坐标为![]() ,不满足题意,舍去.
,不满足题意,舍去.
故直线![]() :
:![]() ,故
,故![]() ,
,![]() ,
,
联立方程得到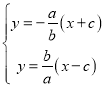 ,解得
,解得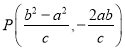 ,
,
代入双曲线方程得到: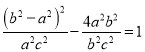 ,化简整理得到:
,化简整理得到:![]() ,故
,故![]() .
.
故答案为:![]() ;
;![]() .
.

练习册系列答案
相关题目