Question

【题目】已知动圆 经过点 ， .
（1）求周长最小的圆的一般方程；
（2）求圆心在直线 上的圆的标准方程.

Answer 1

【答案】
（1）解：当AB为直径时，过A、B的圆的半径最小，从而周长最小．以AB中点(0,1)为圆心，半径r＝ |AB|＝ 的圆的方程为x2＋(y－1)2＝10
（2）解：解法一：直线AB的斜率为k＝－3，则AB的垂直平分线的方程是y－1＝ x，即x－3y＋3＝0，由 得 即圆心是C(3,2)，所以半径r＝|AC|＝ ，所以圆的方程是(x－3)2＋(y－2)2＝20.
解法二：设圆的方程为(x－a)2＋(y－b)2＝r2.
则 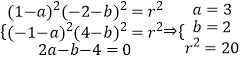所以圆的方程为(x－3)2＋(y－2)2＝20.
【解析】本题给出两个定点A、B，求经过AB周长最小的圆方程，并求圆心在定直线上的圆方程．
利用圆心到直线的d和半径r的关系判断． 圆心到直线的距离d.
①相交：d＜r,
②相切：d=r,
③相离：d＞r.