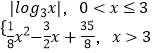题目内容
【题目】已知函数 ![]() .
.
(1)证明 ![]() 有且只有一个零点;
有且只有一个零点;
(2)求这个零点所在的一个区间,使这个区间的长度不大于 ![]() .
.
【答案】
(1)证明:易知f(x)=lnx+2x6在(0,+∞)上是增函数,
∴f(x)至多有一个零点.由于f(2)=ln22<0,f(3)=ln3>0,
∴f(2)·f(3)<0. ∴f(x)在(2,3)内有一个零点.∴f(x)在(0,+∞)上只有一个零点
(2)解:由(1)知f(2)<0,f(3)>0,取 ![]() ,
, ![]() ,
,
∴ ![]() .∴
.∴ ![]() 的零点
的零点 ![]() .取
.取 ![]() ,
,
则 ![]() .
.
∴ ![]() .∴
.∴ ![]() .
.
∵ ![]() ,∴满足题意的区间为
,∴满足题意的区间为 ![]()
【解析】(1)递增函数在某个区间中最多一个零点,而函数的端点处函数值异号时,则有且只有一个零点;
(2)结合二分法及精确度的要求,可求出对应区间.

练习册系列答案
相关题目