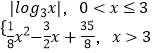题目内容
【题目】已知正方形的中心为直线 ![]() 和
和 ![]() 的交点,正方形一边所在直线的方程为
的交点,正方形一边所在直线的方程为 ![]() ,求其他三边所在直线的方程.
,求其他三边所在直线的方程.
【答案】解:设与直线l:x+3y-5=0平行的边的直线方程为l1:x+3y+c=0.
由 ![]() 得正方形的中心为P(-1,0),由点P到两直线l,l1的距离相等,得
得正方形的中心为P(-1,0),由点P到两直线l,l1的距离相等,得 ![]() =
= ![]() 解得c=7或c=-5(舍去).
解得c=7或c=-5(舍去).
∴l1:x+3y+7=0.又∵正方形另两边所在直线与l垂直,
∴设另两边方程为3x-y+a=0,3x-y+b=0.
∵正方形中心到四条边的距离相等,∴ ![]() ,得a=9或-3,
,得a=9或-3,
∴另两条边所在的直线方程为3x-y+9=0,3x-y-3=0.
∴另三边所在的直线方程分别为3x-y+9=0,x+3y+7=0,3x-y-3=0
【解析】分别设出与已知一边的直线平行与垂直的直线的方程,由正方形的中心到各边的距离相等,求出直线方程.

练习册系列答案
相关题目