题目内容
7.函数f(x)=loga(2x2+x),(a>0,a≠1),若?x∈(0,$\frac{1}{2}$],恒有f(x)>0,解关于x的不等式:f[log2(9x+22x+1+1)]>f[2log4(6x+4x+1+1)].分析 根据题意,由f(x)>0得出0<a<1;判断f(x)在(0,+∞)上是减函数,
由此把所求的不等式化为对数不等式,再根据对数函数的单调性求出x的取值范围即可.
解答 解:∵x∈(0,$\frac{1}{2}$)时,2x2+x∈(0,1),
函数f(x)=loga(2x2+x)在x∈(0,$\frac{1}{2}$)时恒有f(x)>0,
∴0<a<1;
由2x2+x>0,得f(x)的定义域为(-∞,-$\frac{1}{2}$)∪(0+∞);
又∵t=2x2+x在(0,+∞)上是增函数,
y=logat在(0,+∞)上是减函数,
∴函数f(x)=loga(2x2+x)在(0,+∞)上是减函数;
又∵9x+22x+1+1>1,6x+4x+1+1>1,
∴log2(9x+22x+1+1)>0,2log4(6x+4x+1+1)>0;
由f(x)的单调性知,
f(log2(9x+22x+1+1))>f(2log4(6x+4x+1+1))可化为
log2(9x+22x+1+1)<2log4(6x+4x+1+1),
即9x+22x+1+1<6x+4x+1+1,
∴32x+2•22x<2x•3x+4•22x;
∴${(\frac{3}{2})}^{2x}$-${(\frac{3}{2})}^{x}$-2<0,
∴[${(\frac{3}{2})}^{x}$-2][${(\frac{3}{2})}^{x}$+1]<0,
解得-1<${(\frac{3}{2})}^{x}$<2,
即x<${log}_{\frac{3}{2}}$2;
∴不等式的解集为{x|x<${log}_{\frac{3}{2}}$2}.
点评 本题考查了对数函数的性质与应用问题,也考查了不等式的解法与应用问题,是综合性题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
17.运行如下程序框图,如果输入的t∈[-1,3],则输出s属于( )
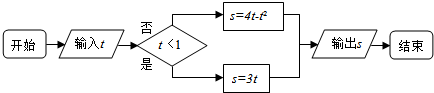

| A. | [-4,3] | B. | [-5,2] | C. | [-3,4] | D. | [-2,5]. |
17.在三角形△ABC中,内角A,B,C所对的边分别为a,b,c,且2c2=2a2+2b2+ab,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
