��Ŀ����
2����������������⣺�ٺ���f��x��=lg��$\sqrt{{x}^{2}+1}$-x����R�ϵ��溯��
�ڰѺ���f��x��=2sin2xͼ����ÿ����ĺ������쳤��ԭ����3����Ȼ��������ƽ��$\frac{��}{6}$����λ���õ��ĺ�������ʽ���Ա�ʾΪg��x��=2sin��$\frac{1}{2}$x-$\frac{��}{6}$��
�ۻ���sin40�㣨tan10��-$\sqrt{3}$�����������1
�ܺ���f��x��=2cos2x����x1��x2���㣺������x����f��x1����f��x����f��x2����������|x1-x2|����СֵΪ$\frac{��}{2}$
����֪��ABC�У�$\overrightarrow{AB}$=��cos18�㣬cos72�㣩��$\overrightarrow{BC}$=��2cos63�㣬2cos27�㣩�����B=135��
������ȷ���������Ǣ٢ܢݣ�������Ϊ��ȷ��������Ŷ����ϣ�
���� �ٸ����溯���Ķ���õ���f��-x��=-f��x����
�ڸ������Ǻ�����ͼ��任�����жϣ�
�۸����л��ҡ����Ǻ͵����ҹ�ʽ�����ǵ����ҹ�ʽ���յ���ʽ����
�ܸ������Ǻ����ĶԳ��Ժ���ֵ�Խ�����Ǻ����������Խ����жϼ��ɣ�
�����������ļнǹ�ʽ�����������㡢ģ�ļ��㹫ʽ�����Ǻ�����ƽ����ϵ�����ǺͲ�����ҹ�ʽ���ɵó���
��� �⣺�١�f��-x��=lg��$\sqrt{{x}^{2}+1}$+x����-f��x��=-lg��$\sqrt{{x}^{2}+1}$-x��=lg$\frac{1}{\sqrt{{x}^{2}+1}-x}$=lg$\frac{\sqrt{{x}^{2}+1}+x}{��\sqrt{{x}^{2}+1��^{2}-{x}^{2}}}$=lg��$\sqrt{{x}^{2}+1}$+x����
��f��-x��=-f��x����
�ຯ��f��x��=lg��$\sqrt{{x}^{2}+1}$-x����R�ϵ��溯����
�ʢ���ȷ��
�ڰѺ���f��x��=2sin2xͼ����ÿ����ĺ������쳤��ԭ����3�����õ�����f��x��=2sin$\frac{2}{3}$x��Ȼ��������ƽ��$\frac{��}{6}$����λ�õ��ĺ�������ʽ���Ա�ʾΪg��x��=2sin$\frac{2}{3}$��x-$\frac{��}{6}$��=2sin��$\frac{2}{3}$x-$\frac{��}{9}$����
�ʢڴ���
��sin40�㣨tan10��-$\sqrt{3}$��=sin40�㣨$\frac{sin10��}{cos10��}$-$\sqrt{3}$��
=-sin40���$\frac{\sqrt{3}cos10��-sin10��}{cos10��}$=-sin40���$\frac{2��\frac{\sqrt{3}}{2}cos10��-\frac{1}{2}sin10�㣩}{cos10��}$=-sin40���$\frac{2cos40��}{cos10��}$=-$\frac{sin80��}{cos10��}$=-1��
�ʢ۴���
��������ʵ��x1��x2��ʹ�ö�����x����f��x1����f��x����f��x2��������
��f��x1��Ϊ����f��x������Сֵ��f��x2��Ϊ����f��x�������ֵ��
��|x1-x2|����СֵΪ$\frac{T}{2}$=$\frac{1}{2}$��$\frac{2��}{2}$=$\frac{��}{2}$��
�ʢ���ȷ��
�ݣ���$\overrightarrow{BA}$•$\overrightarrow{BC}$=-cos18��•2cos63��-cos72��•2cos27��
=-2��sin27��cos18��+cos27��sin18�㣩=-2sin45��=-$\sqrt{2}$��
$\overrightarrow{BA}$=$\sqrt{co{s}^{2}18��+si{n}^{2}18��}$=1��$\overrightarrow{BC}$=$\sqrt{4co{s}^{2}63��+4co{s}^{2}27��}$=2$\sqrt{si{n}^{2}27��+co{s}^{2}27��}$=2��
��cosB=$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BA}|•|\overrightarrow{BC}|}$=$\frac{-\sqrt{2}}{2}$��
���B=135�㣮
�ʢ���ȷ��
������������ȷ�Ľ����Ǣ٢ܢݣ�
�ʴ��ǣ��٢ܢݣ�
���� ������Ҫ�������������жϣ��漰��������Ҫ�����Ǻ�����ͼ��������Լ����Ǻ�����ͼ��任���ۺϿ��������ε����ʵ�Ӧ�ã�

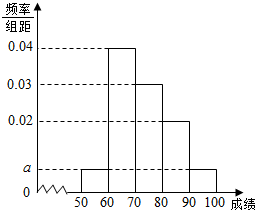 ijУ100��ѧ�����п������ijɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]��
ijУ100��ѧ�����п������ijɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]��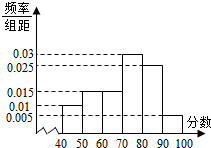 �Ӳμӻ���������ѧ���г��60��������ɼ�����Ϊ��������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���۲�ͼ�Σ��ش��������⣺
�Ӳμӻ���������ѧ���г��60��������ɼ�����Ϊ��������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���۲�ͼ�Σ��ش��������⣺