题目内容
【题目】已知函数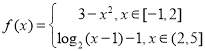 .
.
(1)在直角坐标系内直接画出![]() 的图象;
的图象;
(2)写出![]() 的单调区间,并指出单调性(不要求证明);
的单调区间,并指出单调性(不要求证明);
(3)若函数![]() 有两个不同的零点,求实数
有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)图见解析;(2)在[﹣1,0]上单调递增,在[0,2]上单调递减,在[2,5]上单调递增;(3)(﹣1,1]∪[2,3)
【解析】
(1)直接画出图像得到答案.
(2)根据图像得到函数的单调区间.
(3)变换得到![]() ,讨论
,讨论![]() 的不同取值得到答案.
的不同取值得到答案.
(1)由题意,函数f(x)大致图像如下:
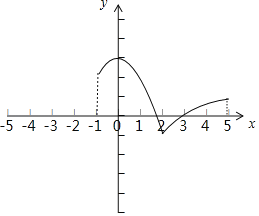
(2)根据(1)中函数f(x)大致图像:
函数f(x)在[﹣1,0]上单调递增,在[0,2]上单调递减,在[2,5]上单调递增.
(3)根据(1)中函数f(x)大致图象,可知
①当t<﹣1时,直线y=t与y=f(x)没有交点;
②当t=﹣1时,直线y=t与y=f(x)有1个交点;
③当﹣1<t≤1时,直线y=t与y=f(x)有2个交点;
④当1<t<2时,直线y=t与y=f(x)有1个交点;
⑤当2≤t<3时,直线y=t与y=f(x)有2个交点;
⑥当t=3时,直线y=t与y=f(x)有1个交点;
⑦当t>3时,直线y=t与y=f(x)没有交点.
∴若函数y=t﹣f(x)有两个不同的零点,实数t的取值范围为:(﹣1,1]∪[2,3).

练习册系列答案
相关题目