题目内容
如图是恩施高中运动场平面图,运动场总面积15000平方米,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,
(Ⅰ)设半圆的半径OA=r(米),写出塑胶跑道面积S与r的函数关系式
S(r);
(Ⅱ)由于受运动场两侧看台限制,r的范围为r∈[30,45],问当r为何值时,运动场造价最低(第2问π取3近似计算).

(Ⅰ)设半圆的半径OA=r(米),写出塑胶跑道面积S与r的函数关系式
S(r);
(Ⅱ)由于受运动场两侧看台限制,r的范围为r∈[30,45],问当r为何值时,运动场造价最低(第2问π取3近似计算).

(Ⅰ)根据题意可得塑胶跑道面积S与r的函数关系式为:
(Ⅱ)总造价y=150S+80(15000-S)
=120000+70S
=120000+560(πr+
-8π),
∵π取3近似计算,
∴y=120000+560(3r+
-24),r∈[30,45],
令t=3r+
,则t′=3-
<0,
∴t=3r+
在区间r∈[30,45]上单调递减,
故当r=45时,总造价最低.
|
(Ⅱ)总造价y=150S+80(15000-S)
=120000+70S
=120000+560(πr+
| 15000 |
| r |
∵π取3近似计算,
∴y=120000+560(3r+
| 15000 |
| r |
令t=3r+
| 15000 |
| r |
| 15000 |
| r2 |
∴t=3r+
| 15000 |
| r |
故当r=45时,总造价最低.

练习册系列答案
相关题目

 内的一个动点,则
内的一个动点,则 的最小值为( ).
的最小值为( ).

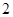
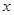 、
、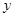 满足线性约束条件
满足线性约束条件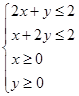 ,则目标函数
,则目标函数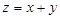 的最大值为 .
的最大值为 . 满足和
满足和 ,则
,则 的取值范围是________.
的取值范围是________.