题目内容
若a>0,b>0,2a+b=2,则下列不等式:
①ab≤1;②
+
≤2;③a2+b2≥2;④8a3+b3≥3;⑤
+
≥2.
对一切满足条件的a,b成立的是( )
①ab≤1;②
| 2a |
| b |
| 1 |
| a |
| 1 |
| b |
对一切满足条件的a,b成立的是( )
| A.①②④ | B.①②⑤ | C.①④⑤ | D.②③④ |
①∵a>0,b>0,2a+b=2,∴2≥2
,∴ab≤
<1,因此成立;
②∵a>0,b>0,2a+b=2,∴(
+
)2≤2[(
)2+(
)2]=2(2a+b)=4,∴
+
≤2,故成立;
③∵a2+b2=a2+(2-2a)2=5(a-
)2+
≥
,当且仅当a=
时取等号,可知③不成立.
④由①可知:2ab<1,∴-6ab>-3.
∴8a3+b3=(2a+b)(4a2+b2-2ab)=(2a+b)[(2a+b)2-6ab]=2(4-6ab)>2×(4+3)=14,故④不成立;
⑤∵a>0,b>0,2a+b=2,∴
+
=
(2a+b)(
+
)=
(3+
+
)≥
(3+2
)=
(3+2
),当且仅当b=
a=2(
-1)时取等号.
而
(3+2
)>2,因此⑤成立.
综上可知:只有①②⑤正确.
故选B.
| 2ab |
| 1 |
| 2 |
②∵a>0,b>0,2a+b=2,∴(
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
③∵a2+b2=a2+(2-2a)2=5(a-
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
④由①可知:2ab<1,∴-6ab>-3.
∴8a3+b3=(2a+b)(4a2+b2-2ab)=(2a+b)[(2a+b)2-6ab]=2(4-6ab)>2×(4+3)=14,故④不成立;
⑤∵a>0,b>0,2a+b=2,∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| b |
| a |
| 2a |
| b |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
而
| 1 |
| 2 |
| 2 |
综上可知:只有①②⑤正确.
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
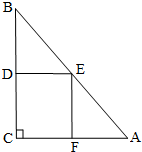

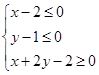 表示的平面区域上运动,则x-y的取值范围是( ).
表示的平面区域上运动,则x-y的取值范围是( ).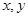 满足约束条件
满足约束条件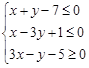 ,则
,则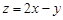 的最大值为( )
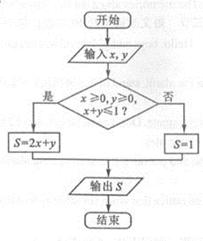
的最大值为( )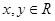 ,则输出的
,则输出的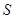 的最大值为( )
的最大值为( )