题目内容
8.经过圆锥高的截面叫圆锥的轴截面,如果经过圆锥的任意两条母线的截面面积的最大值就是轴截面的面积,则圆锥侧面展开得到的扇形中心角的范围是(0,$\sqrt{2}$π].分析 由三角形面积公式分析可得当顶角≤90°时,截面面积的最大,代入数据即可得答案.
解答 解:由题意,经过圆锥的任意两条母线的截面面积的最大值就是轴截面的面积,得到轴截面的顶角≤90°,
所以$\frac{r}{l}$≤$\frac{\sqrt{2}}{2}$,
所以圆锥侧面展开得到的扇形中心角$\frac{2πr}{l}$≤$\sqrt{2}$π,
所以圆锥侧面展开得到的扇形中心角的范围是(0,$\sqrt{2}$π].
故答案为:(0,$\sqrt{2}$π].
点评 本题考查圆锥的轴截面,考查弧长公式,考查学生的计算能力,比较基础.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
3.下列现象的相关程度最高的是( )
| A. | 某商店的职工人数与商品销售额之间的相关系数为0.87 | |
| B. | 流通费用率与商业利润之间的相关系数为-0.94 | |
| C. | 商品销售额与商业利润之间的相关系数为0.51 | |
| D. | 商品销售额与流通费用率之间的相关系数为-0.81 |
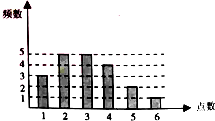 设有动点P,依次沿正方形ABCD的顶点A,B,C,D,A,B…移动,首先以A为出发点,根据一个骰子所掷出的点数移动P,掷出几点移动几步,其次以移动后多到达的点为出发点,再次进行同样的试验.
设有动点P,依次沿正方形ABCD的顶点A,B,C,D,A,B…移动,首先以A为出发点,根据一个骰子所掷出的点数移动P,掷出几点移动几步,其次以移动后多到达的点为出发点,再次进行同样的试验. 在平面直角坐标系xOy中,动点P到定点(1,0)的距离与到定直线x=2的距离之比为$\frac{\sqrt{2}}{2}$,设动点P的轨迹为C.
在平面直角坐标系xOy中,动点P到定点(1,0)的距离与到定直线x=2的距离之比为$\frac{\sqrt{2}}{2}$,设动点P的轨迹为C.