题目内容
17. 在平面直角坐标系xOy中,动点P到定点(1,0)的距离与到定直线x=2的距离之比为$\frac{\sqrt{2}}{2}$,设动点P的轨迹为C.
在平面直角坐标系xOy中,动点P到定点(1,0)的距离与到定直线x=2的距离之比为$\frac{\sqrt{2}}{2}$,设动点P的轨迹为C.(1)求出轨迹C的方程;
(2)设动直线l:y=kx-$\frac{1}{3}$与曲线C交于A、B两点,问在y轴上是否存在定点G,使∠AGB为直角?若存在,求出G的坐标,并求△AGB面积的最大值;若不存在,请说明理由.
分析 (1)设P(x,y),则$\frac{\sqrt{(x-1)^{2}+{y}^{2}}}{|x-2|}$=$\frac{\sqrt{2}}{2}$,化简可得轨迹C的方程;
(2)动直线l:y=kx-$\frac{1}{3}$代入椭圆方程得(2k2+1)x2-$\frac{4}{3}$kx-$\frac{16}{9}$=0.设A(x1,y1),B(x2,y2).利用$\overrightarrow{GA}$•$\overrightarrow{GB}$=0,求出m,表示出面积,配方,求出△GAB面积的最大值.
解答 解:(1)设P(x,y),则$\frac{\sqrt{(x-1)^{2}+{y}^{2}}}{|x-2|}$=$\frac{\sqrt{2}}{2}$,
化简可得$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)动直线l:y=kx-$\frac{1}{3}$代入椭圆方程得(2k2+1)x2-$\frac{4}{3}$kx-$\frac{16}{9}$=0.
设A(x1,y1),B(x2,y2).
则x1+x2=$\frac{4k}{3(2{k}^{2}+1)}$,x1x2=-$\frac{16}{9(2{k}^{2}+1)}$
假设在y上存在定点G(0,m),满足题设,
则$\overrightarrow{GA}$•$\overrightarrow{GB}$=x1x2+(y1-m)(y2-m)=(k2+1)x1x2-k($\frac{1}{3}$+m)(x1+x2)+m2+$\frac{2}{3}$m+$\frac{1}{9}$
=$\frac{18({m}^{2}-1){k}^{2}+(9{m}^{2}+6m-15)}{9(2{k}^{2}+1)}$=0.
∴$\left\{\begin{array}{l}{{m}^{2}-1=0}\\{9{m}^{2}+6m-15=0}\end{array}\right.$,
解得m=1.
故在y轴上存在定点G(0,1),使得以AB为直径的圆恒过这个点…(10分)
这时,点G到AB的距离d=$\frac{4}{3\sqrt{{k}^{2}+1}}$,
|AB|=$\sqrt{1+{k}^{2}}$•|x1-x2|,
∴S△GAB=$\frac{1}{2}$|AB|d=$\frac{2}{3}$•|x1-x2|=$\frac{8}{9}\sqrt{\frac{{9k}^{2}+4}{(2{k}^{2}+1)^{2}}}$
设2k2+1=t,则k2=$\frac{t-1}{2}$(t≥1).
∴S△GAB=$\frac{8}{9}$$\sqrt{\frac{1}{2}[\frac{81}{4}-(\frac{1}{t}-\frac{9}{2})^{2}}$≤$\frac{16}{9}$.
当且仅当t=1时,上式等号成立.
因此,△GAB面积的最大值是$\frac{16}{9}$.
点评 通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.本题有一定的探索性.综合性强,难度大,易出错.

 阅读快车系列答案
阅读快车系列答案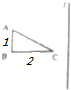 如图所示,直角△ABC,∠B=90°,AB=1,BC=2,直线l⊥BC,若将△ABC绕直线l旋转一周,得到的几何体的体积是$\frac{8}{3}π$.
如图所示,直角△ABC,∠B=90°,AB=1,BC=2,直线l⊥BC,若将△ABC绕直线l旋转一周,得到的几何体的体积是$\frac{8}{3}π$.