题目内容
【题目】求下列函数的最值
（1）求函数
的最小值.
（2）求函数
的最小值.
（3）设
，
，若
，求
的最小值.
（4）若正数
，
满足
，求
的最小值.
【答案】（1）
.（2）
.（3）
.（4）
【解析】
（1）先将函数表达式转化为
，再由基本不等式求得函数的最小值.
（2）先将函数表达式转化为
，再由基本不等式求得函数的最小值.
（3）先将所求表达式转化为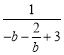
，再由基本不等式求得最小值.
（4）利用“
”的代换的方法，化简所求表达式，再由基本不等式求得最小值.
（1）
，故函数
的最小值为，当且仅当
，即
时取得；
（2）
，故函数的最小值为，当且仅当
即
时取得；
（3）由题得
，代入原式，得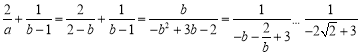
，故原式的最小值为，当且仅当
，即
时取得；
（4）由题得
，则
，当且仅当
时取“
”，故最小值为5.
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
【题目】假设关于某设备的使用年限
和所支出的维修费用
（万元）有如下的统计资料：
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知对呈线性相关关系．
（1）请画出上表数据的散点图；
（2）请根据最小二乘法求出线性回归方程
的回归系数
．
（3）估计使用年限为10年时，维修费用是多少？
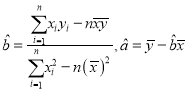
【题目】某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验．选取两大块地，每大块地分成
小块地，在总共
小块地中．随机选
小块地种植品种甲，另外
小块地种植品种乙．
（
）假设
，求第一大块地都种植品种甲的概率．
（
）试验时每大块地分成
小块．即
，试验结束后得到品种甲和品种乙在各个小块地上的每公顷产量（单位
）如下表：
品种甲 |
|
|
|
|
|
品种乙 |
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？
