题目内容
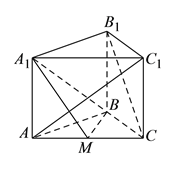
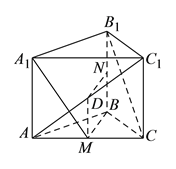
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() 为棱
为棱![]() 中点.
中点. ![]() ,
, ![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() .
.
(II)求证: ![]() 平面
平面![]() .
.
(III)在棱![]() 的上是否存在点
的上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求此时
?如果存在,求此时![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
【答案】(I)见解析;(II)见解析;(III)见解析.
【解析】试题分析:(Ⅰ)连结AB1交A1B于O,连结OM,可证OM∥B1C,又OM平面A1BM,B1C平面A1BM,即可证明B1C∥平面A1BM.
(Ⅱ)易证AA1⊥BM,又可证BM⊥AC1,由AC=2,AM=1,![]() ,可求∠AC1C+∠C1AC=∠A1MA+∠C1AC=90°,从而可证A1M⊥AC1,从而证明AC1⊥平面A1BM.
,可求∠AC1C+∠C1AC=∠A1MA+∠C1AC=90°,从而可证A1M⊥AC1,从而证明AC1⊥平面A1BM.
(Ⅲ)当点N为BB1中点时,可证平面AC1N⊥平面AA1C1C,设AC1中点为D,连结DM,DN,可证BM∥DN,由BM⊥平面ACC1A1,可证DN⊥平面ACC1A1,即可证明平面AC1N⊥平面ACC1A1.
试题解析:
(I)证明:连接![]() 交
交![]() 于
于![]() 点,
点,
连接![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 中点,
中点,
∴![]() .
.
又∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(II)∵![]() 底面
底面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() 为棱
为棱![]() 中点,
中点,
![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 中点,
中点, ![]() ,
,
∴![]() ,
,
又∵![]() .
.
在![]() 与
与![]() 中,
中,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
∴![]() 平面
平面![]() .
.
(III)存在点![]() ,当
,当![]() 时成立,
时成立,
设![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() ,
,
∵![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 中点,
中点,
∴![]() ,
,
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() .
.
∴平面![]() 平面
平面![]() .
.

练习册系列答案
相关题目