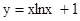题目内容
已知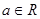 ,讨论函数
,讨论函数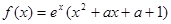 的极值点的个数
的极值点的个数
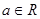 ,讨论函数
,讨论函数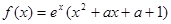 的极值点的个数
的极值点的个数当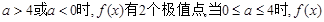 无极值点
无极值点
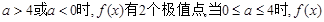 无极值点
无极值点【错解分析】利用一阶导数求函数的极大值和极小值的方法是导数在研究函数性质方面的继续深入 是导数应用的关键知识点,通过对函数极值的判定,可使学生加深对函数单调性与其导数关系的理解.
【正解】
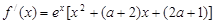 令
令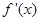 =0得
=0得 .
.(1)当
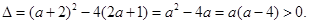 即
即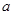 <0或
<0或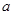 >4时
>4时 有两个不同的实根
有两个不同的实根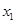 ,
,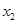 ,
,不妨设
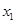 <
<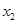 ,则
,则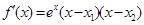 ,
,易判断
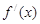 在
在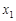 和
和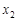 两侧的符号都相反,即此时
两侧的符号都相反,即此时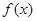 有两个极值点.
有两个极值点.(2)当△=0即
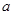 =0或
=0或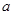 =4时,方程
=4时,方程 有两个相同的实根
有两个相同的实根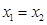 ,于是
,于是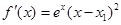 ,故在
,故在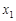 的两侧均有
的两侧均有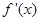 >0,因此
>0,因此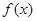 无极值.
无极值.(3)当△<0即0<
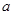 <4时
<4时 无实数根,
无实数根,即
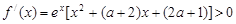 ,
,故
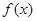 为增函数,此时
为增函数,此时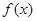 无极值.
无极值.综上所述:当
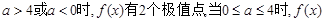 无极值点.
无极值点.【点评】此题考查的是可导函数在某点取得极值的充要条件,即:设
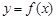 在某个区间内可导,函数
在某个区间内可导,函数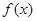 在某点取得极值的充要条件是该点的导数为零且在该点两侧的导数值异号.本题从逆向思维的角度出发,根据题设结构进行逆向联想,合理地实现了问题的转化,使抽象的问题具体化
在某点取得极值的充要条件是该点的导数为零且在该点两侧的导数值异号.本题从逆向思维的角度出发,根据题设结构进行逆向联想,合理地实现了问题的转化,使抽象的问题具体化
练习册系列答案
相关题目
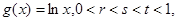 则( )
则( )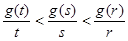
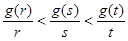
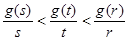
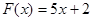 (
(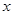 单位为
单位为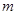 ,
,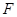 单位为
单位为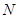 )的作用下,沿着与力
)的作用下,沿着与力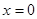 处运动到
处运动到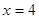 处,则力
处,则力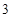
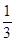
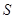 (米)与时间
(米)与时间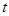 (秒)的关系是
(秒)的关系是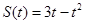 ,则物体在
,则物体在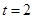 秒时的瞬时速度为( )
秒时的瞬时速度为( ) m/s
m/s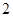 m/s
m/s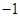 m/s
m/s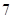 m/s
m/s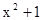 在(1,2)处的切线斜率为( )
在(1,2)处的切线斜率为( )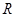 上的函数
上的函数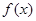 满足
满足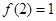 ,且
,且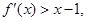 则不等式
则不等式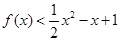 的解集为( )
的解集为( )

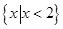
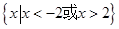
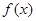 满足
满足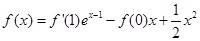 ,则
,则