题目内容
【题目】已知函数![]() 在
在![]() 时取得极值且
时取得极值且![]() 有两个零点.
有两个零点.
(1)求![]() 的值与实数
的值与实数![]() 的取值范围;
的取值范围;
(2)记函数![]() 两个相异零点
两个相异零点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先对函数求导,根据极值点求出![]() ,得到函数解析式,再由
,得到函数解析式,再由![]() 有两个零点,得到方程
有两个零点,得到方程![]() 有2个不同实根,令
有2个不同实根,令![]() ,根据导数的方法研究
,根据导数的方法研究![]() 单调性与最值,即可求出
单调性与最值,即可求出![]() 的取值范围;
的取值范围;
(2)利用函数零点的性质,结合函数单调性和导数之间的关系,进行转化即可证明不等式.
(1)因为![]() ,所以
,所以![]() ,
,
又![]() 在
在![]() 时取得极值,所以
时取得极值,所以![]() ,即
,即![]() ;
;
所以![]() ,
,
因为![]() 有两个零点,所以方程
有两个零点,所以方程![]() 有2个不同实根,
有2个不同实根,
令![]() ,则
,则![]() ,
,
由![]() 得
得![]() ;由
;由![]() 得
得![]() ;
;
所以函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减,
上单调递减,
所以![]() ,又
,又![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;
因此,要使方程![]() 有2个不同实根,只需
有2个不同实根,只需![]() 与
与![]() 有两不同交点,
有两不同交点,
所以![]() ;
;
(2)因为函数![]() 两个相异零点
两个相异零点![]() ,所以
,所以![]() ,
,![]() ①;
①;
即![]() ,即
,即![]() ②;
②;
又![]() 等价于
等价于![]() ,即
,即![]() ③;
③;
由①②③可得![]() ;
;
不妨令![]() ,则
,则![]() ,
,
上式可化为![]() ;
;
设![]() ,则
,则![]() 在
在![]() 上恒成立;
上恒成立;
故函数![]() 在
在![]() 上单调递增;
上单调递增;
所以![]() ,即不等式
,即不等式![]() 成立;
成立;
因此,所证不等式![]() 成立.
成立.

【题目】“微信运动”已经成为当下热门的健身方式,韩梅梅的微信朋友圈内有800为好友参与了“微信运动”.他随机抽取了50为微信好友(男、女各25人),统计其在某一天的走路步数.其中女性好友的走路步数数据记录如下:
12860 8320 10231 6734 7323 8430 3200 4543 11123 9860
8753 6454 7292 4850 10222 9734 7944 9117 6421 2980
1123 1786 2436 3876 4326
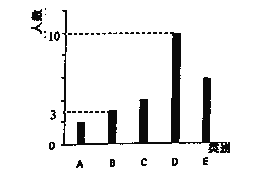
男性好友走路步数情况可以分为五个类别![]() (0-2000步)(说明:“0-2000”表示大于等于0,小于等于2000,下同),
(0-2000步)(说明:“0-2000”表示大于等于0,小于等于2000,下同),![]() (2001-5000)、
(2001-5000)、![]() (5001-8000)、
(5001-8000)、![]() (8001-10000步)、
(8001-10000步)、![]() (10001步及以上),且
(10001步及以上),且![]() 三中类型的人数比例为
三中类型的人数比例为![]() ,将统计结果绘制如图所示的柱形图.
,将统计结果绘制如图所示的柱形图.
若某人一天的走路步数超过8000步则被系统评定为“积极型”,否则被系统评定为“懈怠型”.
(1)若以韩梅梅抽取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计韩梅梅的微信好友圈里参与“微信运动”的800名好友中,每天走路步数在5001-10000步的人数;
(2)请根据选取的样本数据完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | 25 | ||
女 | 25 | ||
总计 | 30 |
(3)若从韩梅梅当天选取的步数大于10000的好友中按男女比例分层选取5人进行身体状况调查,然后再从这5位好友中选取2人进行访谈,求至少有一位女性好友访谈的概率.
参考公式: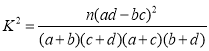 ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |