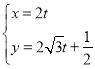题目内容
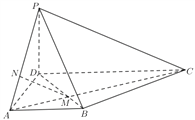
【题目】在四棱锥![]() 中,
中,![]()
![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() ,且
,且![]() 平面
平面![]() .
.
(1)求实数![]() 的值;
的值;
(2)若![]() ,
,![]() , 求点
, 求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:解法一:(1)由平行线的性质可得![]() ,结合线面平行的性质定理有
,结合线面平行的性质定理有![]() .据此可得
.据此可得![]() .
.
(2) 由题意可知![]() 为等边三角形,则
为等边三角形,则![]() ,结合勾股定理可知
,结合勾股定理可知![]() 且
且![]() ,由线面垂直的判断定理有
,由线面垂直的判断定理有![]() 平面
平面![]() ,进一步有平面
,进一步有平面![]() 平面
平面![]() .作
.作![]() 于
于![]() ,则
,则![]() 平面
平面![]() .
. ![]() 即为
即为![]() 到平面
到平面![]() 的距离.结合比例关系计算可得
的距离.结合比例关系计算可得![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二:(1)同解法一.
(2)由题意可得![]() 为等边三角形,所以
为等边三角形,所以![]() ,结合勾股定理可得
,结合勾股定理可得![]() 且
且![]() ,则
,则![]() 平面
平面![]() .设点
.设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,利用体积关系:
,利用体积关系:![]() , 即
, 即![]() .求解三角形的面积然后解方程可得
.求解三角形的面积然后解方程可得![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
详解:解法一:(1)因为![]() ,所以
,所以![]() 即
即![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
所以![]() .
.
所以![]() ,即
,即![]() .
.
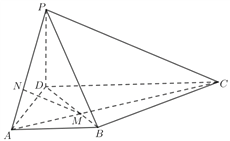
(2) 因为![]() ,所以
,所以![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
又因为![]() ,
,![]() ,所以
,所以![]() 且
且![]() ,
,
所以![]() 且
且![]() ,又因为
,又因为![]() ,所以
,所以![]()
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
作![]() 于
于![]() ,因为平面
,因为平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() 即为
即为![]() 到平面
到平面![]() 的距离.
的距离.
在△![]() 中,设
中,设![]() 边上的高为
边上的高为![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二、(1)同解法一.
(2)因为![]() ,所以
,所以![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
又因为![]() ,
,![]() ,所以
,所以![]() 且
且![]() ,
,
所以![]() 且
且![]() ,又因为
,又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() 得
得![]() ,
,
所以![]() ,
,
即![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,解得
,解得![]() ,即
,即![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目