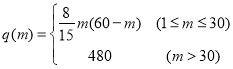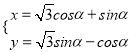题目内容
【题目】已知函数![]() (
(![]() 是非零实常数)满足
是非零实常数)满足![]() 且方程
且方程![]() 有且仅有一个实数解.
有且仅有一个实数解.
(1)求![]() 的值
的值
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围
的取值范围
(3)在直角坐标系中,求定点![]() 到函数
到函数![]() 图像上的任意一点
图像上的任意一点![]() 的距离
的距离![]() 的最小值,并求取得最小值时
的最小值,并求取得最小值时![]() 的值
的值
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]() 取得最小值,最小值为
取得最小值,最小值为![]()
【解析】
(1)由![]() 可得
可得![]() ;将
;将![]() 化为
化为![]() ,由方程仅有一个实数解可确定
,由方程仅有一个实数解可确定![]() ,从而求得
,从而求得![]() ;
;
(2)将不等式化为![]() 对
对![]() 恒成立,分别在
恒成立,分别在![]() 、
、![]() 和
和![]() 三种情况下,采用分离变量的方式求得
三种情况下,采用分离变量的方式求得![]() 的取值范围,进而得到结果;
的取值范围,进而得到结果;
(3)设![]() ,由两点间距离公式可整理得
,由两点间距离公式可整理得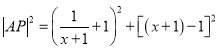 ,令
,令![]() 可得到
可得到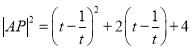 ,根据二次函数的性质可求得最值点和最值.
,根据二次函数的性质可求得最值点和最值.
(1)![]()
![]() ,即
,即![]()
![]()
由![]() 得:
得:![]()
![]() 有且仅有一个实数解
有且仅有一个实数解 ![]() ,解得:
,解得:![]()
![]()
(2)由(1)知:![]()
![]() 可化为:
可化为:
即![]() 对
对![]() 恒成立
恒成立
当![]() 时,不等式为
时,不等式为![]() ,显然不成立,不合题意;
,显然不成立,不合题意;
当![]() 时,
时,![]()
![]()
![]() ,解得:
,解得:![]() ;
;
当![]() 时,
时,![]()
![]()
![]() ,解集为
,解集为![]() ;
;
综上所述:![]() 的取值范围为
的取值范围为![]()
(3)设![]()
则
令![]() ,则
,则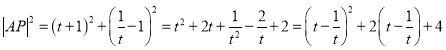
当![]() ,即
,即![]() 时,
时,![]()
![]() 当
当![]() 或
或![]() ,即
,即![]() 或
或![]() 时,
时,![]() 取得最小值,最小值为
取得最小值,最小值为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目