题目内容
(本小题满分14分)已知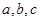 是互不相等的实数,
是互不相等的实数,
求证:由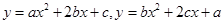 和
和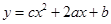 确定的三条抛物线至少有一条与
确定的三条抛物线至少有一条与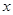 轴有两个不同的交点.
轴有两个不同的交点.
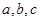 是互不相等的实数,
是互不相等的实数,求证:由
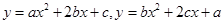 和
和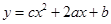 确定的三条抛物线至少有一条与
确定的三条抛物线至少有一条与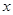 轴有两个不同的交点.
轴有两个不同的交点.见解析.
至少有一条与
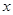 轴有两个不同的交点,情况比较多,用正难则反原则,假设题设中的函数确定的三条抛物线都不与
轴有两个不同的交点,情况比较多,用正难则反原则,假设题设中的函数确定的三条抛物线都不与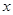 轴有两个不同的交点,解之。
轴有两个不同的交点,解之。证明:假设题设中的函数确定的三条抛物线都不与
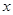 轴有两个不同的交点,即任何一条抛物线与
轴有两个不同的交点,即任何一条抛物线与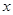 轴没有两个不同的交点┈┈┈┈┈┈┈┈┈┈┈┈2分
轴没有两个不同的交点┈┈┈┈┈┈┈┈┈┈┈┈2分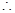
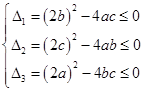 ┈┈┈┈┈┈┈┈┈┈┈┈3分
┈┈┈┈┈┈┈┈┈┈┈┈3分相加得
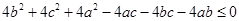 ┈┈┈┈┈┈┈┈┈┈┈┈2分
┈┈┈┈┈┈┈┈┈┈┈┈2分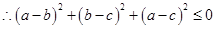 ┈┈┈┈┈┈┈┈┈┈┈┈4分
┈┈┈┈┈┈┈┈┈┈┈┈4分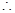
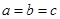 与题设
与题设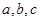 互不相等矛盾. ┈┈┈┈┈┈┈┈┈┈┈2分
互不相等矛盾. ┈┈┈┈┈┈┈┈┈┈┈2分因此假设不成立,从而命题的证. ┈┈┈┈┈┈┈┈┈┈┈┈1分

练习册系列答案
相关题目
 ,且其三个顶点均在抛物线E:x2=2py(p>0)上.
,且其三个顶点均在抛物线E:x2=2py(p>0)上.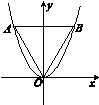
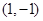 为中点的抛物线
为中点的抛物线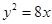 的弦所在直线方程为: .
的弦所在直线方程为: .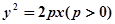 的所有焦点弦中,弦长的最小值为( )
的所有焦点弦中,弦长的最小值为( )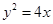 的焦点
的焦点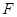 的直线交该抛物线于
的直线交该抛物线于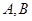 两点,若
两点,若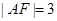 ,则
,则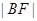 =______
=______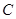 过点
过点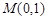 且与直线
且与直线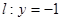 相切,设圆心
相切,设圆心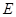 ,
,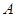 、
、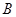 为曲线
为曲线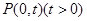 ,且满足
,且满足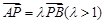 .
.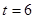 ,直线
,直线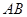 的斜率为
的斜率为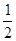 ,过
,过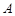 、
、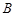 两点的圆
两点的圆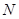 与抛物线在点
与抛物线在点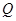 ,若点
,若点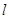 上,求证:
上,求证: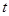 与
与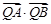 均为定值.
均为定值.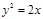 与过焦点的直线l交于A、B两点,则
与过焦点的直线l交于A、B两点,则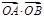 等于( ).
等于( ).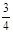 B.
B. 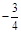 C. 3 D. -2
C. 3 D. -2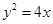 的焦点
的焦点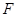 的直线交抛物线于
的直线交抛物线于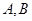 两点,点
两点,点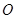 是原点,若
是原点,若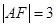 ;则
;则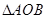 的面积为( )
的面积为( )