题目内容
以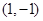 为中点的抛物线
为中点的抛物线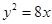 的弦所在直线方程为: .
的弦所在直线方程为: .
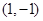 为中点的抛物线
为中点的抛物线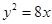 的弦所在直线方程为: .
的弦所在直线方程为: .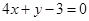
解:此弦不垂直于X轴,故设点(1,-1)为中点的抛物线y2=8x的弦的两端点为A(x1,yi)B(x2,y2)
得到yi2=8x1,y22=8x2
两式相减得到(yi+ y2)(yi- y2)=8(x1-x2)
∴k=yi- y2 / x1-x2 =-4
∴直线方程为y+1=-4(x-1),即4x+y-3=0
得到yi2=8x1,y22=8x2
两式相减得到(yi+ y2)(yi- y2)=8(x1-x2)
∴k=yi- y2 / x1-x2 =-4
∴直线方程为y+1=-4(x-1),即4x+y-3=0

练习册系列答案
相关题目
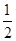 )到抛物线C:y
)到抛物线C:y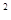 =2px(P>0)的准线的距离为
=2px(P>0)的准线的距离为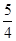 .点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.
.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.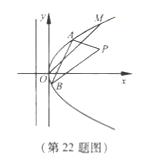
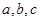 是互不相等的实数,
是互不相等的实数,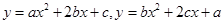 和
和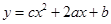 确定的三条抛物线至少有一条与
确定的三条抛物线至少有一条与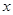 轴有两个不同的交点.
轴有两个不同的交点.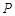 为抛物线C:
为抛物线C: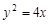 上的一点,
上的一点,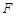 为抛物线C的焦点,其准线与
为抛物线C的焦点,其准线与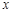 轴交于点
轴交于点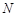 ,直线
,直线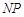 与抛物线交于另一点
与抛物线交于另一点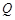 ,且
,且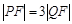 ,则点
,则点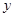 轴的右侧运动,它到
轴的右侧运动,它到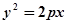 的准线
的准线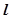 ,焦点为
,焦点为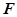 ,顶点为
,顶点为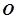 ,
,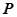 为抛物线上任意一点,
为抛物线上任意一点,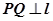 ,
,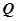 为垂足,求
为垂足,求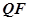 与
与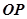 的交点
的交点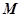 的轨迹方程.
的轨迹方程.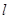 过抛物线
过抛物线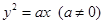 的焦点
的焦点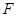 ,且和
,且和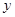 轴交于点
轴交于点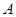 ,若
,若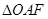 (
(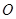 为坐标原点)的面积为4,则抛物线方程为( )
为坐标原点)的面积为4,则抛物线方程为( ) 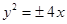
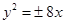
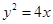

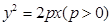 的焦点为F,过点F作直线
的焦点为F,过点F作直线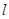 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与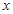 轴交于点C。
轴交于点C。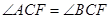 ;
;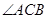 的最大值,并求
的最大值,并求