题目内容
若圆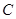 过点
过点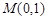 且与直线
且与直线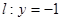 相切,设圆心
相切,设圆心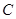 的轨迹为曲线
的轨迹为曲线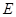 ,
,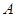 、
、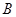 为曲线
为曲线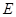 上的两点,点
上的两点,点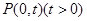 ,且满足
,且满足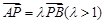 .
.
(1)求曲线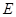 的方程;
的方程;
(2)若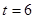 ,直线
,直线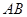 的斜率为
的斜率为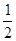 ,过
,过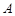 、
、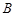 两点的圆
两点的圆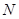 与抛物线在点
与抛物线在点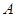 处有共同的切线,求圆
处有共同的切线,求圆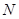 的方程;
的方程;
(3)分别过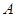 、
、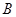 作曲线
作曲线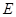 的切线,两条切线交于点
的切线,两条切线交于点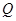 ,若点
,若点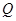 恰好在直线
恰好在直线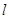 上,求证:
上,求证: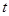 与
与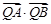 均为定值.
均为定值.
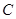 过点
过点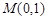 且与直线
且与直线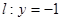 相切,设圆心
相切,设圆心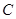 的轨迹为曲线
的轨迹为曲线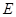 ,
,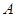 、
、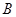 为曲线
为曲线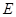 上的两点,点
上的两点,点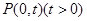 ,且满足
,且满足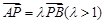 .
.(1)求曲线
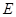 的方程;
的方程;(2)若
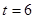 ,直线
,直线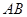 的斜率为
的斜率为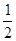 ,过
,过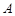 、
、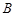 两点的圆
两点的圆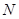 与抛物线在点
与抛物线在点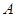 处有共同的切线,求圆
处有共同的切线,求圆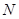 的方程;
的方程;(3)分别过
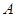 、
、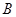 作曲线
作曲线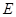 的切线,两条切线交于点
的切线,两条切线交于点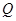 ,若点
,若点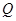 恰好在直线
恰好在直线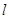 上,求证:
上,求证: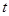 与
与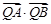 均为定值.
均为定值.(1)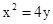 ;(2)
;(2)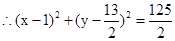 ;(3)0.
;(3)0.
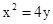 ;(2)
;(2)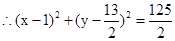 ;(3)0.
;(3)0.本试题主要考查了直线与圆的位置关系,以及直线与抛物线的位置关系的综合运用。
(1)依题意,点C到定点M的距离等于到定直线L的距离,所以点C的轨迹为抛物线,曲线E的方程为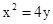 ;
;
(2)直线AB的方程是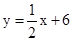 ,即x-2y+12=0,
,即x-2y+12=0,
由联立x-2y+12=0和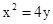 ,得点A、B、、的坐标是(6,9)或(-4,4),
,得点A、B、、的坐标是(6,9)或(-4,4),
当A(6,9)或B(-4,4),时,由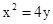 得
得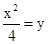 ,
,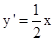 ,
,
所以抛物线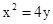 在点A处切线的斜率为
在点A处切线的斜率为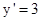 ,
,
直线NA的方程为 ,即x+3y-33=0…………①
,即x+3y-33=0…………①
线段AB的中点坐标为(1,13/2),中垂线方程为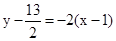 ,…………②
,…………②
由①、②解得,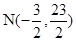
于是,圆C的方程为
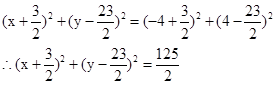 ,
,
当B(6,9)或A(-4,4),时,抛物线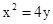 在点A处切线的斜率为
在点A处切线的斜率为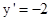 ,此时切线与AB垂直,所求圆为以AB为直径的圆,可求得圆为
,此时切线与AB垂直,所求圆为以AB为直径的圆,可求得圆为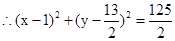 ,
,
(3)设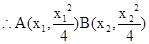 ,,Q(a,-1),过点A的切线方程为
,,Q(a,-1),过点A的切线方程为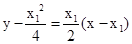 ,
,
即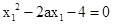 ,同理可得
,同理可得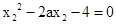 ,所以
,所以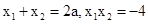 ,,
,,
又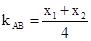 ,所以直线
,所以直线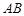 的方程为
的方程为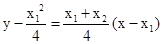 ,
,
亦即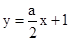 ,所以t=1,
,所以t=1,
而 ,,所以
,,所以
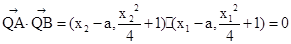
(1)依题意,点C到定点M的距离等于到定直线L的距离,所以点C的轨迹为抛物线,曲线E的方程为
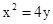 ;
; (2)直线AB的方程是
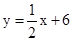 ,即x-2y+12=0,
,即x-2y+12=0,由联立x-2y+12=0和
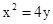 ,得点A、B、、的坐标是(6,9)或(-4,4),
,得点A、B、、的坐标是(6,9)或(-4,4),当A(6,9)或B(-4,4),时,由
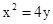 得
得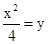 ,
,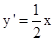 ,
,所以抛物线
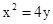 在点A处切线的斜率为
在点A处切线的斜率为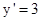 ,
,直线NA的方程为
 ,即x+3y-33=0…………①
,即x+3y-33=0…………①线段AB的中点坐标为(1,13/2),中垂线方程为
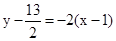 ,…………②
,…………②由①、②解得,
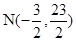
于是,圆C的方程为
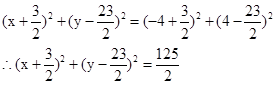 ,
,当B(6,9)或A(-4,4),时,抛物线
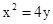 在点A处切线的斜率为
在点A处切线的斜率为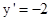 ,此时切线与AB垂直,所求圆为以AB为直径的圆,可求得圆为
,此时切线与AB垂直,所求圆为以AB为直径的圆,可求得圆为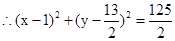 ,
, (3)设
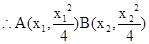 ,,Q(a,-1),过点A的切线方程为
,,Q(a,-1),过点A的切线方程为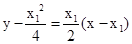 ,
,即
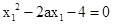 ,同理可得
,同理可得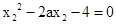 ,所以
,所以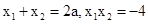 ,,
,,又
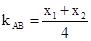 ,所以直线
,所以直线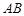 的方程为
的方程为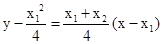 ,
,亦即
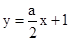 ,所以t=1,
,所以t=1,而
 ,,所以
,,所以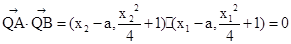

练习册系列答案
相关题目
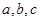 是互不相等的实数,
是互不相等的实数,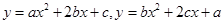 和
和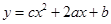 确定的三条抛物线至少有一条与
确定的三条抛物线至少有一条与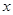 轴有两个不同的交点.
轴有两个不同的交点.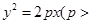

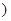 的对称轴上的定点
的对称轴上的定点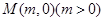 ,作直线
,作直线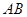 与抛物线相交于
与抛物线相交于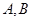 两点.
两点.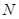 是定直线
是定直线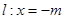 上的任一点,试探索三条直线
上的任一点,试探索三条直线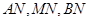 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.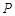 为抛物线C:
为抛物线C: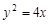 上的一点,
上的一点,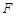 为抛物线C的焦点,其准线与
为抛物线C的焦点,其准线与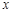 轴交于点
轴交于点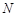 ,直线
,直线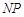 与抛物线交于另一点
与抛物线交于另一点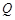 ,且
,且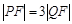 ,则点
,则点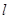 过抛物线
过抛物线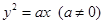 的焦点
的焦点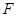 ,且和
,且和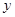 轴交于点
轴交于点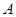 ,若
,若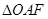 (
(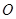 为坐标原点)的面积为4,则抛物线方程为( )
为坐标原点)的面积为4,则抛物线方程为( ) 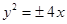
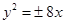
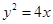

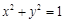 与抛物线
与抛物线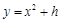 有公共点,则实数h的取值范围是
有公共点,则实数h的取值范围是  为过抛物线
为过抛物线 焦点
焦点 的一条弦,设
的一条弦,设 ,以下结论正确的是____________________,
,以下结论正确的是____________________, 且
且 ②
② 的最小值为
的最小值为 ③以
③以 为直径的圆与
为直径的圆与 轴相切;
轴相切; 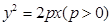 的焦点为F,过点F作直线
的焦点为F,过点F作直线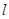 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与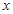 轴交于点C。
轴交于点C。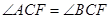 ;
;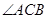 的最大值,并求
的最大值,并求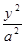 -
-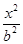 =1(a>0, b>0)有相同的焦点F,点B是两曲线的一个交点,且BF⊥y轴,若L为双曲线的一条渐近线,则L的倾斜角所在的区间可能是 ( )
=1(a>0, b>0)有相同的焦点F,点B是两曲线的一个交点,且BF⊥y轴,若L为双曲线的一条渐近线,则L的倾斜角所在的区间可能是 ( )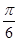 ,
,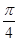 )
)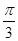 )
)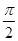 ,
,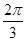 )
)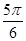 ,π)
,π)