题目内容
2.在△ABC中,BC=1,B=$\frac{π}{3}$,当△ABC的面积等于$\sqrt{3}$时,sinC等于( )| A. | $\frac{{2\sqrt{39}}}{13}$ | B. | $\frac{{\sqrt{13}}}{13}$ | C. | $\frac{{2\sqrt{39}}}{3}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
分析 由△ABC的面积 求出c,再由余弦定理求出b,再由正弦定理求出sinC=$\frac{csinB}{b}$的值.
解答 解:∵由△ABC的面积$\sqrt{3}$=$\frac{1}{2}$acsin$\frac{π}{3}$,a=1,可得:c=4,
再由余弦定理可得:b2=a2+c2-2accosB=1+16-2×1×4×$\frac{1}{2}$=13,可得b=$\sqrt{13}$.
再由正弦定理可得:$\frac{4}{sinC}=\frac{\sqrt{13}}{sin\frac{π}{3}}$,
∴解得:sinC=$\frac{2\sqrt{39}}{13}$,
故选:A.
点评 本题主要考查了正弦定理、余弦定理的应用,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
14.已知函数y=2x2-2x+1的导数为y′,y′=( )
| A. | 2x-2 | B. | 4x+1 | C. | 4x-2 | D. | 2x+1 |
13.下列式子中,错误的是( )
| A. | $(\frac{1}{x})'=-\frac{1}{x^2}$ | B. | (cos(2x+1))′=-2sin(2x+1) | ||
| C. | $(x{log_a}x)'={log_a}x+\frac{1}{lna}$ | D. | $(\frac{{e}^{x}}{x})′=\frac{{e}^{x}•x+{e}^{x}}{{x}^{2}}$ |
7.如图所示,平面内z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,则|z1+z2|=( )
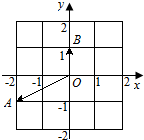

| A. | 2 | B. | 3 | C. | 2 $\sqrt{2}$ | D. | 3 $\sqrt{3}$ |
11.在(2x2-x-1)5的二项展开式中,x的系数为( )
| A. | 10 | B. | -10 | C. | 40 | D. | -40 |
12.在△ABC中,不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$≥$\frac{9}{π}$成立;在四边形ABCD中,不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$≥$\frac{16}{2π}$成立;在五边形ABCDE中,$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$+$\frac{1}{E}$≥$\frac{25}{3π}$成立.猜想在n边形中,成立的不等式为( )
| A. | $\frac{1}{{A}_{1}}$+$\frac{1}{{A}_{2}}$+…$\frac{1}{{A}_{n}}$≥$\frac{n}{π}$ | B. | $\frac{1}{{A}_{1}}$+$\frac{1}{{A}_{2}}$+…$\frac{1}{{A}_{n}}$≥$\frac{{n}^{2}}{(n+1)π}$ | ||
| C. | $\frac{1}{{A}_{1}}$+$\frac{1}{{A}_{2}}$+…$\frac{1}{{A}_{n}}$≥$\frac{{n}^{2}}{(n-2)π}$ | D. | $\frac{1}{{A}_{1}}$+$\frac{1}{{A}_{2}}$+…$\frac{1}{{A}_{n}}$≥$\frac{{n}^{2}}{(n+2)π}$ |