题目内容
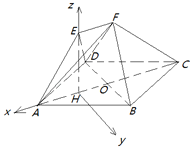
【题目】如图,多面体EF﹣ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)若直线AE与平面ABCD所成的角为45°,求平面DEF与平面ABCD所成角(锐角)的余弦值.

【答案】(1)见解析(2)![]()
【解析】分析:(Ⅰ)取AO的中点H,连结EH,证明EH⊥BD,AC⊥BD,即BD⊥平面ACF
(Ⅱ)由(Ⅰ)知EH⊥平面ABCD,以H为原点,如图所示建立空间直角坐标系H﹣xyz,
由EH⊥平面ABCD,得∠EAH为AE与平面ABCD所成的角,即∠EAH=45°则
![]() 求出平面DEF与平面ABCD的法向量,代入公式即可求解.
求出平面DEF与平面ABCD的法向量,代入公式即可求解.
详解:(Ⅰ)取AO的中点H,连结EH,则EH⊥平面ABCD
∵BD在平面ABCD内,∴EH⊥BD
又菱形ABCD中,AC⊥BD 且EH∩AC=H,EH、AC在平面EACF内
∴BD⊥平面EACF,即BD⊥平面ACF
(Ⅱ)由(Ⅰ)知EH⊥平面ABCD,以H为原点,如图所示建立空间直角坐标系H﹣xyz
∵EH⊥平面ABCD,∴∠EAH为AE与平面ABCD所成的角,
即∠EAH=45°,又菱形ABCD的边长为4,则![]()
各点坐标分别为![]() ,
,
E(0,0,![]() )
)
易知![]() 为平面ABCD的一个法向量,记
为平面ABCD的一个法向量,记![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]()
∵EF∥AC,∴![]() =
=![]()
设平面DEF的一个法向量为![]() (注意:此处
(注意:此处![]() 可以用
可以用![]() 替代)
替代)
即 ![]() =
=![]() ,
,![]()
令![]() ,则,∴
,则,∴![]()
∴![]()
平面DEF与平面ABCD所成角(锐角)的余弦值为![]() .
.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目




