Question

【题目】定义新运算：当m≥n时，mn＝m；当m＜n时，mn＝n．设函数f（x）＝[（2x2）﹣（1log2x）]2x，则f（x）在（0，2）上值域为______．

Answer 1

【答案】

【解析】

根据题意即可得出，x≥1时，2x2＝2x；x＜1时，2x2＝2；0＜x≤2时，1log2x＝1；x＞2时，1log2x＝log2x，从而得出0＜x＜1时，f（x）＝2x，从而求出1＜f（x）＜2；1≤x＜2时，f（x）＝22x﹣2x，配方即可求出2≤f（x）＜12，这样即可得出f（x）在（0，2）上的值域．

根据题意，2x≥2，即x≥1时，2x2＝2x；2x＜2，即x＜1时，2x2＝2；1≥log2x，即0＜x≤2时，1log2x＝1；1＜log2x，即x＞2时，1log2x＝log2x；

∴；

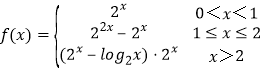∴①0＜x＜1时，f（x）＝2x是增函数；

∴1＜f（x）＜2；

②1≤x＜2时，；

∵1≤x＜2；

∴2≤2x＜4；

∴；

∴2≤f（x）＜12；

综上得，f（x）在（0，2）上的值域为（1，12）．

故答案为：（1，12）．