题目内容
【题目】已知函数
， 
，且直线
是函数
的一条切线．
（Ⅰ）求
的值；
（Ⅱ）对任意的
，都存在
，使得
，求
的取值范围；
（Ⅲ）已知方程
有两个根
（
），若
，求证： 
．
【答案】（Ⅰ）
;（Ⅱ）
;（Ⅲ）
．
【解析】试题分析：（Ⅰ）设切点，由题意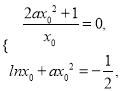得
解得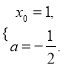
（Ⅱ）由题意可得f(x)的值域是g(x)的值域的子集，可得
，
解得
．
（Ⅲ）依题意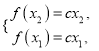得
两式相减得
， 进而方程
可转化为则
，令
， 
，证得
，所以
，即
．
试题解析：（Ⅰ）设直线
与
相切于点
，
，
依题意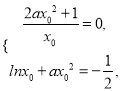得
解得
所以
，经检验： 
符合题意
（Ⅱ）由（Ⅰ）得
，所以
，
当
时， 
所以
在
上单调递减，
所以当
时， 
， 
，
，
当
时， 
，所以
在
上单调递增，
所以当
时， 
， 
，
依题意得
，
所以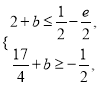
解得
．
（Ⅲ）依题意得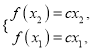
两式相减得
，
所以
，
方程
可转化为
，
即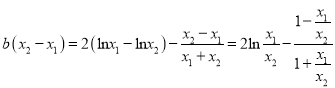
，
令
，则
，则
，
令
， 
，
因为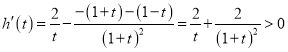
，
所以
在
上单调递增，所以
，
所以
，即
．
点晴：本题主要考查函数导数与单调性，函数导数研究图象与性质等知识.首先画出两个函数的图象，由此来理解题意“对
， 
，使得
”，根据图象，将问题等价变形为对于相同的函数值，两个函数对应的自变量的距离的最小值来求.构造函数后利用导数研究函数的单调性，由此求得最值.
练习册系列答案
相关题目
