题目内容
【题目】已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2 , a4的等差中项
①求数列{an}的通项公式;
②设bn=anlog2an , 求数列{bn}的前n项和Sn .
【答案】解:①∵a3+2是a2 , a4的等差中项,
∴2(a3+2)=a2+a4 ,
即 ![]() ,
,
又a2+a3+a4=28,
即 ![]() ,
,
∴q= ![]() (舍去)或q=2,
(舍去)或q=2,
∴a1=2,
∴an=2n .
②由①知an=2n .
∴bn=anlog2an=n2n ,
∴ ![]() ,
,![]()
∴两式相减得, ![]() ,
,
即 ![]()
【解析】①根据条件,建立方程组即可求出数列{an}的通项公式;②利用错位相减法求出数列的前n项和Sn
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系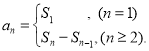 ).
).

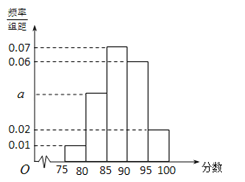
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.
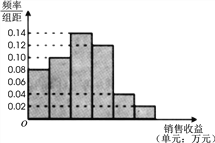
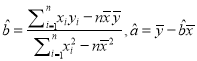
【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的![]() 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温![]() (
(![]() )与该奶茶店的
)与该奶茶店的![]() 品牌饮料销量
品牌饮料销量![]() (杯),得到如表数据:
(杯),得到如表数据:
日期 | 1月11号 | 1月12号 | 1月13号 | 1月14号 | 1月15号 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程式
的线性回归方程式![]() ;
;
(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)